Finite Difference Methods for the Poisson Equation with Zero Boundary

This notebook will focus on numerically approximating a inhomogenous second order Poisson Equation with zero boundary conditions.

The Differential Equation

The general two dimensional Poisson Equation is of the form:

(705)\[\begin{equation} \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial x^2}=f(x,y), \ \ \ (x,y) \in \Omega=(0,1)\times (0,1),\end{equation}\]

with boundary conditions

(706)\[\begin{equation}U(x,y) = g(x,y), \ \ \ (x,y)\in\delta\Omega\text{ - boundary}. \end{equation}\]

Homogenous Poisson Equation

This notebook will implement a finite difference scheme to approximate the inhomogenous form of the Poisson Equation \(f(x,y)=x^2+y^2\), with a zero boundary:

(707)\[\begin{equation} \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial x^2}=x^2+y^2.\end{equation}\]

with the Boundary Conditions:

(708)\[\begin{equation} u(x,0)=0, \ \ \ \ \ 0 \leq x \leq 1, \text{ lower},\end{equation}\]

(709)\[\begin{equation} u(x,1)=0, \ \ \ \ \ 0 \leq x \leq 1, \text{ upper},\end{equation}\]

(710)\[\begin{equation} u(0,y)=0, \ \ \ \ \ 0 \leq y \leq 1, \text{ left},\end{equation}\]

(711)\[\begin{equation} u(1,y)=0, \ \ \ \ \ 0 \leq y \leq 1, \text{ right}.\end{equation}\]

# LIBRARY
# vector manipulation
import numpy as np
# math functions
import math 

# THIS IS FOR PLOTTING
%matplotlib inline
import matplotlib.pyplot as plt # side-stepping mpl backend
import warnings
warnings.filterwarnings("ignore")
from IPython.display import HTML
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt

Discete Grid

The region \(\Omega=(0,1)\times(0,1)\) is discretised into a uniform mesh \(\Omega_h\). In the \(x\) and \(y\) directions into \(N\) steps giving a stepsize of

(712)\[\begin{equation} h=\frac{1-0}{N},\end{equation}\]

resulting in

(713)\[\begin{equation}x[i]=0+ih, \ \ \ i=0,1,...,N,\end{equation}\]

and

(714)\[\begin{equation}x[j]=0+jh, \ \ \ j=0,1,...,N,\end{equation}\]

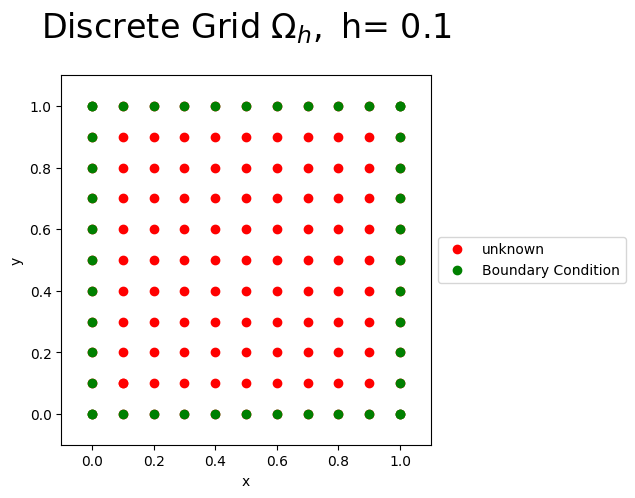
The Figure below shows the discrete grid points for \(N=10\), the known boundary conditions (green), and the unknown values (red) of the Poisson Equation.

N=10
h=1/N
x=np.arange(0,1.0001,h)
y=np.arange(0,1.0001,h)
X, Y = np.meshgrid(x, y)
fig = plt.figure()
plt.plot(x[1],y[1],'ro',label='unknown');
plt.plot(X,Y,'ro');
plt.plot(np.ones(N+1),y,'go',label='Boundary Condition');
plt.plot(np.zeros(N+1),y,'go');
plt.plot(x,np.zeros(N+1),'go');
plt.plot(x, np.ones(N+1),'go');
plt.xlim((-0.1,1.1))
plt.ylim((-0.1,1.1))
plt.xlabel('x')
plt.ylabel('y')
plt.gca().set_aspect('equal', adjustable='box')
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.title(r'Discrete Grid $\Omega_h,$ h= %s'%(h),fontsize=24,y=1.08)
plt.show();

Boundary Conditions

The discrete boundary conditions are

(715)\[\begin{equation} w[i,0]=0, \text{ for } i=0,...,10, \text{ upper},\end{equation}\]

(716)\[\begin{equation} w[i,N]=0, \text{ for } i=0,...,10, \text{ lower},\end{equation}\]

(717)\[\begin{equation} w[0,j]=0, \text{ for } j=0,...,10, \text{ left},\end{equation}\]

(718)\[\begin{equation} w[N,j]=0, \text{ for } i=0,...,10,\text{ right}. \end{equation}\]

The Figure below plots the boundary values of \(w[i,j]\).

w=np.zeros((N+1,N+1))

for i in range (0,N):
        w[i,0]=0 #left Boundary
        w[i,N]=0 #Right Boundary

for j in range (0,N):
        w[0,j]=0 #Lower Boundary
        w[N,j]=0 #Upper Boundary

        
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Plot a basic wireframe.
ax.plot_wireframe(X, Y, w,color='r', rstride=10, cstride=10)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('w')
plt.title(r'Boundary Values',fontsize=24,y=1.08)
plt.show()

Numerical Method

The Poisson Equation is discretised using \(\delta_x^2\) is the central difference approximation of the second derivative in the \(x\) direction

(719)\[\begin{equation}\delta_x^2=\frac{1}{h^2}(w_{i+1j}-2w_{ij}+w_{i-1j}), \end{equation}\]

and \(\delta_y^2\) is the central difference approximation of the second derivative in the \(y\) direction

(720)\[\begin{equation}\delta_y^2=\frac{1}{h^2}(w_{ij+1}-2w_{ij}+w_{ij-1}). \end{equation}\]

The gives the Poisson Difference Equation,

(721)\[\begin{equation}-(\delta_x^2w_{ij}+\delta_y^2w_{ij})=f_{ij} \ \ (x_i,y_j) \in \Omega_h, \end{equation}\]

(722)\[\begin{equation}w_{ij}=g_{ij} \ \ (x_i,y_j) \in \partial\Omega_h, \end{equation}\]

where \(w_ij\) is the numerical approximation of \(U\) at \(x_i\) and \(y_j\). Expanding the the Poisson Difference Equation gives the five point method,

(723)\[\begin{equation}-(w_{i-1j}+w_{ij-1}-4w_{ij}+w_{ij+1}+w_{i+1j})=h^2f_{ij} \end{equation}\]

for \(i=1,...,N-1\) and \(j=1,...,N-1.\)

Matrix form

This can be written as a system of \((N-1)\times(N-1)\) equations can be arranged in matrix form

(724)\[\begin{equation} A\mathbf{w}=\mathbf{r},\end{equation}\]

where \(A\) is an \((N-1)^2\times(N-1)^2\) matrix made up of the following block tridiagonal structure

(725)\[\begin{equation}\left(\begin{array}{ccccccc} T&I&0&0&.&.&.\\ I&T&I&0&0&.&.\\ .&.&.&.&.&.&.\\ .&.&.&0&I&T&I\\ .&.&.&.&0&I&T\\ \end{array}\right), \end{equation}\]

where \(I\) denotes an \(N-1 \times N-1\) identity matrix and \(T\) is the tridiagonal matrix of the form:

(726)\[\begin{equation} T=\left(\begin{array}{ccccccc} -4&1&0&0&.&.&.\\ 1&-4&1&0&0&.&.\\ .&.&.&.&.&.&.\\ .&.&.&0&1&-4&1\\ .&.&.&.&0&1&-4\\ \end{array}\right). \end{equation}\]

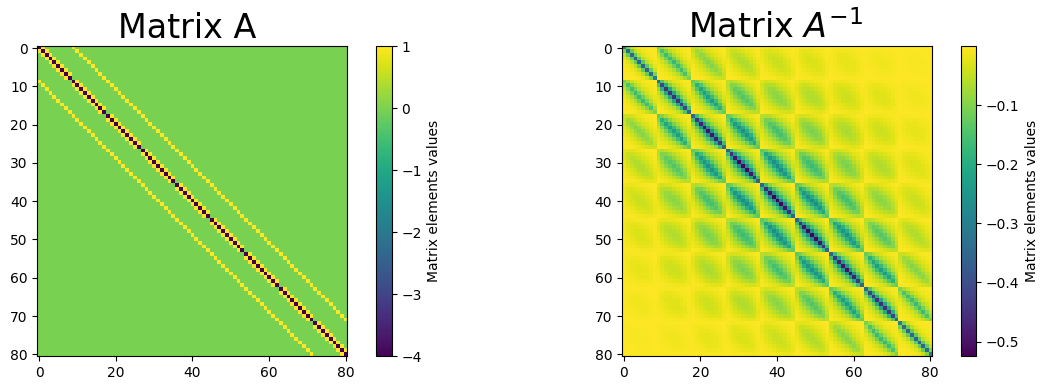
The plot below shows the matrix \(A\) and its inverse \(A^{-1}\) as a colourplot.

N2=(N-1)*(N-1)
A=np.zeros((N2,N2))
## Diagonal            
for i in range (0,N-1):
    for j in range (0,N-1):           
        A[i+(N-1)*j,i+(N-1)*j]=-4

# LOWER DIAGONAL        
for i in range (1,N-1):
    for j in range (0,N-1):           
        A[i+(N-1)*j,i+(N-1)*j-1]=1   
# UPPPER DIAGONAL        
for i in range (0,N-2):
    for j in range (0,N-1):           
        A[i+(N-1)*j,i+(N-1)*j+1]=1   

# LOWER IDENTITY MATRIX
for i in range (0,N-1):
    for j in range (1,N-1):           
        A[i+(N-1)*j,i+(N-1)*(j-1)]=1        
        
        
# UPPER IDENTITY MATRIX
for i in range (0,N-1):
    for j in range (0,N-2):           
        A[i+(N-1)*j,i+(N-1)*(j+1)]=1
Ainv=np.linalg.inv(A)   
fig = plt.figure(figsize=(12,4));
plt.subplot(121)
plt.imshow(A,interpolation='none');
clb=plt.colorbar();
clb.set_label('Matrix elements values');
plt.title('Matrix A ',fontsize=24)
plt.subplot(122)
plt.imshow(Ainv,interpolation='none');
clb=plt.colorbar();
clb.set_label('Matrix elements values');
plt.title(r'Matrix $A^{-1}$ ',fontsize=24)

fig.tight_layout()
plt.show();

The vector \(\mathbf{w}\) is of length \((N-1)\times(N-1)\) which made up of \(N-1\) subvectors \(\mathbf{w}_j\) of length \(N-1\) of the form

(727)\[\begin{equation}\mathbf{w}_j=\left(\begin{array}{c} w_{1j}\\ w_{2j}\\ .\\ .\\ w_{N-2j}\\ w_{N-1j}\\ \end{array}\right). \end{equation}\]

The vector \(\mathbf{r}\) is of length \((N-1)\times(N-1)\) which made up of \(N-1\) subvectors of the form \(\mathbf{r}_j=-h^2\mathbf{f}_j-\mathbf{bx}_{j}-\mathbf{by}_j\). In this example the boundary is \(0\) which means that

(728)\[\begin{equation}\mathbf{bx}_j =0,\end{equation}\]

(729)\[\begin{equation} \mathbf{by}_{j} =0, \end{equation}\]

and

(730)\[\begin{equation}\mathbf{f}_j =\left(\begin{array}{c} x_1^2+y_j^2\\ x_2^2+y_j^2\\ .\\ .\\ x_{N-2}^2+y_j^2\\ x_{N-1}^2+y_j^2\\ \end{array}\right) \end{equation}\]

for \(j=1,...,N-1\).

r=np.zeros(N2)

# vector r      
for i in range (0,N-1):
    for j in range (0,N-1):           
        r[i+(N-1)*j]=h*h*(x[i]*x[i]+y[j]*y[j])     
# Boundary        
b_bottom_top=np.zeros(N2)
for i in range (0,N-1):
    b_bottom_top[i]=0 #Bottom Boundary
    b_bottom_top[i+(N-1)*(N-2)]=0# Top Boundary
      
b_left_right=np.zeros(N2)
for j in range (0,N-1):
    b_left_right[(N-1)*j]=0 # Left Boundary
    b_left_right[N-2+(N-1)*j]=0# Right Boundary
    
b=b_left_right+b_bottom_top

Results

To solve the system for \(\mathbf{w}\) invert the matrix \(A\)

(731)\[\begin{equation} A\mathbf{w}=\mathbf{r},\end{equation}\]

such that

(732)\[\begin{equation} \mathbf{w}=A^{-1}\mathbf{r}.\end{equation}\]

Lastly, as \(\mathbf{w}\) is in vector it has to be reshaped into grid form to plot.

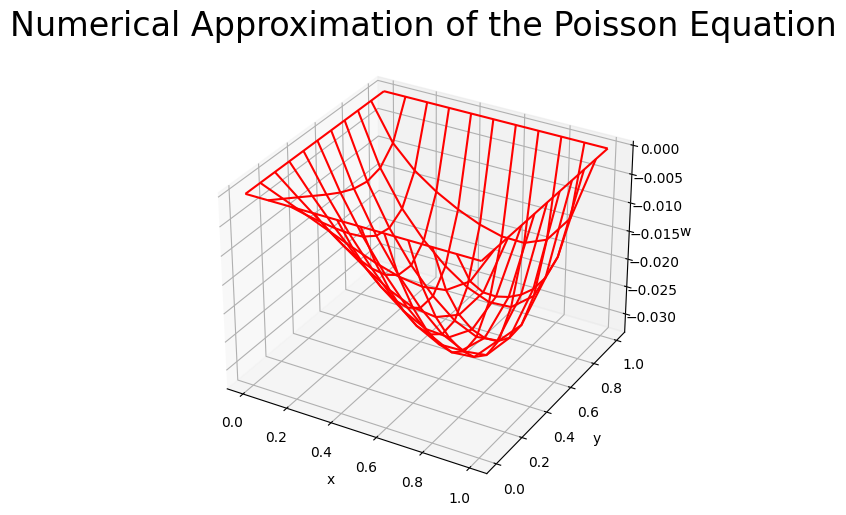
The figure below shows the numerical approximation of the homogeneous Equation.

C=np.dot(Ainv,r-b)
w[1:N,1:N]=C.reshape((N-1,N-1))

fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d');
# Plot a basic wireframe.
ax.plot_wireframe(X, Y, w,color='r');
ax.set_xlabel('x');
ax.set_ylabel('y');
ax.set_zlabel('w');
plt.title(r'Numerical Approximation of the Poisson Equation',fontsize=24,y=1.08);
plt.show();

Consistency and Convergence

We now ask how well the grid function determined by the five point scheme approximates the exact solution of the Poisson problem.

Consistency

Consitency (Definition)

Let

(733)\[\begin{equation}\nabla^2_h(\varphi)=-(\varphi_{i-1j}+\varphi_{ij-1}-4\varphi_{ij}+\varphi_{ij+1}+\varphi_{i+1j})\end{equation}\]

denote the finite difference approximation associated with the grid \(\Omega_h\) having the mesh size \(h\), to a partial differential operator

(734)\[\begin{equation}\nabla^2(\varphi)=\frac{\partial^2 \varphi}{\partial x^2}+\frac{\partial^2 \varphi}{\partial y^2}\end{equation}\]

a simply connected, open set \(\Omega \subset R^2\). For a given function \(\varphi\in C^{\infty}(\Omega)\), the truncation error of \(\nabla^2_h\) is

(735)\[\begin{equation}\tau_{h}(\mathbf{x})=(\nabla^2-\nabla^2_h)\varphi(\mathbf{x}) \end{equation}\]

The approximation \(\nabla^2_h\) is consistent with \(\nabla^2\) if

(736)\[\begin{equation}\lim_{h\rightarrow 0}\tau_h(\mathbf{x})=0,\end{equation}\]

for all \(\mathbf{x} \in D\) and all \(\varphi \in C^{\infty}(\Omega)\). The approximation is consistent to order \(p\) if \(\tau_h(\mathbf{x})=O(h^p)\).

In other words a method is consistent with the differential equation it is approximating.

Proof of Consistency

The five-point difference analog \(\nabla^2_h\) is consistent to order 2 with \(\nabla^2\).

Proof

Pick \(\varphi \in C^{\infty}(D)\), and let \((x,y) \in \Omega\) be a point such that \((x\pm h, y),(x,y \pm h) \in \Omega\bigcup \partial\Omega\). By the Taylor Theorem

\[\begin{eqnarray*} \varphi(x\pm h,y)&=&\varphi(x,y) \pm h \frac{\partial \varphi}{\partial x}(x,y)+\frac{h^2}{2!}\frac{\partial^2 \varphi}{\partial x^2}(x,y) \pm\frac{h^3}{3!}\frac{\partial^3 \varphi}{\partial x^3}(x,y)+\frac{h^4}{4!}\frac{\partial^4 \varphi}{\partial x^4}(\zeta^{\pm},y) \end{eqnarray*}\]

where \(\zeta^{\pm} \in (x-h,x+h)\). Adding this pair of equation together and rearranging , we get

(737)\[\begin{equation}\frac{1}{h^2}[\varphi(x+h,y)-2\varphi(x,y)+\varphi(x-h,y) ] -\frac{\partial^2 \varphi}{\partial x^2}(x,y)=\frac{h^2}{4!}\left[\frac{\partial^4 \varphi}{\partial x^4}(\zeta^{+},y)+ \frac{\partial^4 \varphi}{\partial x^4}(\zeta^{-},y) \right] \end{equation}\]

By the intermediate value theorem \end{equation}\left[\frac{\partial^4 \varphi}{\partial x^4}(\zeta^{+},y)+ \frac{\partial^4 \varphi}{\partial x^4}(\zeta^{-},y) \right] =2\frac{\partial^4 \varphi}{\partial x^4}(\zeta,y),\end{equation} for some \(\zeta \in (x-h,x+h)\). Therefore,

(738)\[\begin{equation}\delta_x^2(x,y) =\frac{\partial^2 \varphi}{\partial x^2}(x,y)+\frac{h^2}{2!}\frac{\partial^4 \varphi}{\partial x^4}(\zeta,y)\end{equation}\]

Similar reasoning shows that

(739)\[\begin{equation}\delta_y^2(x,y) =\frac{\partial^2 \varphi}{\partial y^2}(x,y)+\frac{h^2}{2!}\frac{\partial^4 \varphi}{\partial y^4}(x,\eta) \end{equation}\]

for some \(\eta \in (y-h,y+h)\). We conclude that \(\tau_h(x,y)=(\nabla-\nabla_h)\varphi(x,y)=O(h^2).\)

Convergence

Definition

Let \(\nabla^2_hw(\mathbf{x}_j)=f(\mathbf{x}_j)\) be a finite difference approximation, defined on a grid mesh size \(h\), to a PDE \(\nabla^2U(\mathbf{x})=f(\mathbf{x})\) on a simply connected set \(D \subset R^n\). Assume that \(w(x,y)=U(x,y)\) at all points \((x,y)\) on the boundary \(\partial\Omega\). The finite difference scheme converges (or is convergent) if \end{equation} \max_j|U(\mathbf{x}_j)-w(\mathbf{x}_j)| \rightarrow 0 \mbox{ as } h \rightarrow 0.\end{equation}

Theorem (DISCRETE MAXIMUM PRINCIPLE).

If \(\nabla^2_hV_{ij}\geq 0\) for all points \((x_i,y_j) \in \Omega_h\), then

(740)\[\begin{equation} \max_{(x_i,y_j)\in\Omega_h}V_{ij}\leq \max_{(x_i,y_j)\in\partial\Omega_h}V_{ij},\end{equation}\]

If \(\nabla^2_hV_{ij}\leq 0\) for all points \((x_i,y_j) \in \Omega_h\), then

(741)\[\begin{equation} \min_{(x_i,y_j)\in\Omega_h}V_{ij}\geq \min_{(x_i,y_j)\in\partial\Omega_h}V_{ij}.\end{equation}\]

Propositions

1. The zero grid function for which \(U_{ij}=0\) for all \((x_i,y_j) \in \Omega_h \bigcup \partial\Omega_h\) is the only solution to the finite difference problem

(742)\[\begin{equation}\nabla_h^2U_{ij}=0 \mbox{ for }(x_i,y_j)\in\Omega_h,\end{equation}\]

(743)\[\begin{equation}U_{ij}=0 \mbox{ for }(x_i,y_j)\in\partial\Omega_h.\end{equation}\]

2. For prescribed grid functions \(f_{ij}\) and \(g_{ij}\), there exists a unique solution to the problem

(744)\[\begin{equation}\nabla_h^2U_{ij}=f_{ij} \mbox{ for }(x_i,y_j)\in\Omega_h,\end{equation}\]

(745)\[\begin{equation}U_{ij}=g_{ij} \mbox{ for }(x_i,y_j)\in\partial\Omega_h.\end{equation}\]

Definition

For any grid function \(V:\Omega_h\bigcup\partial\Omega_h \rightarrow R\),

(746)\[\begin{equation}||V||_{\Omega} =\max_{(x_i,y_j)\in\Omega_h}|V_{ij}|, \end{equation}\]

(747)\[\begin{equation}||V||_{\partial\Omega} =\max_{(x_i,y_j)\in\partial\Omega_h}|V_{ij}|. \end{equation}\]

Lemma

If the grid function \(V:\Omega_h\bigcup\partial\Omega_h\rightarrow R\) satisfies the boundary condition \(V_{ij}=0\) for \((x_i,y_j)\in \partial\Omega_h\), then

(748)\[\begin{equation}||V_||_{\Omega}\leq \frac{1}{8}||\nabla_h^2V||_{\Omega}. \end{equation}\]

Given these Lemmas and Propositions, we can now prove that the solution to the five point scheme \(\nabla^2_h\) is convergent to the exact solution of the Poisson Equation \(\nabla^2\).

Convergence Theorem

Let \(U\) be a solution to the Poisson equation and let \(w\) be the grid function that satisfies the discrete analog

(749)\[\begin{equation}-\nabla_h^2w_{ij}=f_{ij} \ \ \mbox{ for } (x_i,y_j)\in\Omega_h, \end{equation}\]

(750)\[\begin{equation}w_{ij}=g_{ij} \ \ \mbox{ for } (x_i,y_j)\in\partial\Omega_h. \end{equation}\]

Then there exists a positive constant \(K\) such that

(751)\[\begin{equation}||U-w||_{\Omega}\leq KMh^2, \end{equation}\]

where

(752)\[\begin{equation} M=\left\{ \left|\left|\frac{\partial^4 U}{\partial x^4} \right|\right|_{\infty}, \left|\left|\frac{\partial^4 U}{\partial y^4} \right|\right|_{\infty} \right\}\end{equation}\]

Proof

The statement of the theorem assumes that \(U\in C^4(\bar{\Omega})\). This assumption holds if \(f\) and \(g\) are smooth enough. \begin{proof} Following from the proof of the Proposition we have

(753)\[\begin{equation} (\nabla_h^2-\nabla^2)U_{ij}=\frac{h^2}{12}\left[ \frac{\partial^4 U}{\partial x^4}(\zeta_i,y_j)+\frac{\partial^4 U}{\partial y^4}(x_i,\eta_j) \right],\end{equation}\]

for some \(\zeta \in (x_{i-1},x_{i+1})\) and \(\eta_j\in(y_{j-1},y_{j+1})\). Therefore,

(754)\[\begin{equation} -\nabla_h^2U_{ij}=f_{ij}-\frac{h^2}{12}\left[ \frac{\partial^4 U}{\partial x^4}(\zeta_i,y_j)+\frac{\partial^4 U}{\partial y^4}(x_i,\eta_j) \right].\end{equation}\]

If we subtract from this the identity equation \(-\nabla_h^2w_{ij}=f_{ij}\) and note that \(U-w\) vanishes on \(\partial\Omega_h\), we find that

(755)\[\begin{equation} \nabla_h^2(U_{ij}-w_{ij})=\frac{h^2}{12}\left[ \frac{\partial^4 U}{\partial x^4}(\zeta_i,y_j)+\frac{\partial^4 U}{\partial y^4}(x_i,\eta_j) \right].\end{equation}\]

It follows that

(756)\[\begin{equation} ||U-w||_{\Omega}\leq\frac{1}{8}||\nabla_h^2(U-w)||_{\Omega}\leq KMh^2.\end{equation}\]