The Implicit Crank-Nicolson Difference Equation for the Heat Equation

John S Butler john.s.butler@tudublin.ie Course Notes Github

Overview

This notebook will illustrate the Crank-Nicolson Difference method for the Heat Equation.

The Heat Equation

The Heat Equation is the first order in time (\(t\)) and second order in space (\(x\)) Partial Differential Equation:

(595)\[\begin{equation} \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2},\end{equation}\]

The equation describes heat transfer on a domain

(596)\[\begin{equation} \Omega = \{ t \geq, 0\leq x \leq 1\}. \end{equation}\]

with an initial condition at time \(t=0\) for all \(x\) and boundary condition on the left (\(x=0\)) and right side

This notebook will illustrate the Crank-Nicolson Difference method for the Heat Equation with the initial conditions

(597)\[\begin{equation} u(x,0)=2x, \ \ 0 \leq x \leq \frac{1}{2}, \end{equation}\]

(598)\[\begin{equation} u(x,0)=2(1-x), \ \ \frac{1}{2} \leq x \leq 1, \end{equation}\]

and boundary condition

(599)\[\begin{equation} u(0,t)=0, u(1,t)=0. \end{equation}\]

Crank-Nicolson Difference method

The implicit Crank-Nicolson difference equation of the Heat Equation is derived by discretising the

(600)\[\begin{equation} \frac{\partial u_{ij+\frac{1}{2}}}{\partial t} = \frac{\partial^2 u_{ij+\frac{1}{2}}}{\partial x^2},\end{equation}\]

around \((x_i,t_{j+\frac{1}{2}})\) giving the difference equation

(601)\[\begin{equation} \frac{w_{ij+1}-w_{ij}}{k}=\frac{1}{2}\left(\frac{w_{i+1j+1}-2w_{ij+1}+w_{i-1j+1}}{h^2}+\frac{w_{i+1j}-2w_{ij}+w_{i-1j}}{h^2}\right). \end{equation}\]

Rearranging give the difference equation

(602)\[\begin{equation} -rw_{i-1j+1}+(2+2r)w_{ij+1}-rw_{i+1j+1}=rw_{i-1j}+(2-2r)w_{ij}+rw_{i+1j} \end{equation}\]

for \(i=1,...9\) where \(r=\frac{k}{h^2}\).

# LIBRARY
# vector manipulation
import numpy as np
# math functions
import math 

# THIS IS FOR PLOTTING
%matplotlib inline
import matplotlib.pyplot as plt # side-stepping mpl backend
import warnings
warnings.filterwarnings("ignore")

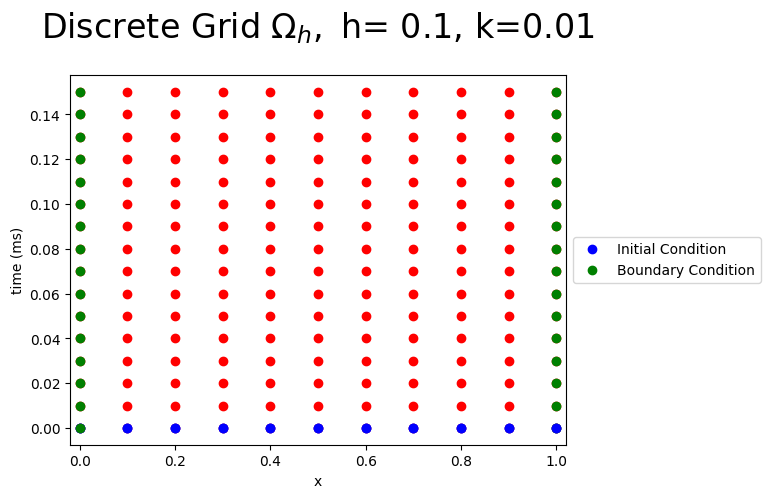
Discete Grid

The region \(\Omega\) is discretised into a uniform mesh \(\Omega_h\). In the space \(x\) direction into \(N\) steps giving a stepsize of

(603)\[\begin{equation} h=\frac{1-0}{N},\end{equation}\]

resulting in

(604)\[\begin{equation}x[i]=0+ih, \ \ \ i=0,1,...,N,\end{equation}\]

and into \(N_t\) steps in the time \(t\) direction giving a stepsize of

(605)\[\begin{equation} k=\frac{1-0}{N_t}\end{equation}\]

resulting in

(606)\[\begin{equation}t[i]=0+ik, \ \ \ k=0,...,K.\end{equation}\]

The Figure below shows the discrete grid points for \(N=10\) and \(N_t=100\) , the red dots are the unknown values, the green dots are the known boundary conditions and the blue dots are the known initial conditions of the Heat Equation.

N=10
Nt=100
h=1/N
k=1/Nt
r=k/(h*h)
time_steps=15
time=np.arange(0,(time_steps+.5)*k,k)
x=np.arange(0,1.0001,h)
X, Y = np.meshgrid(x, time)
fig = plt.figure()
plt.plot(X,Y,'ro');
plt.plot(x,0*x,'bo',label='Initial Condition');
plt.plot(np.ones(time_steps+1),time,'go',label='Boundary Condition');
plt.plot(x,0*x,'bo');
plt.plot(0*time,time,'go');
plt.xlim((-0.02,1.02))
plt.xlabel('x')
plt.ylabel('time (ms)')
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.title(r'Discrete Grid $\Omega_h,$ h= %s, k=%s'%(h,k),fontsize=24,y=1.08)
plt.show();

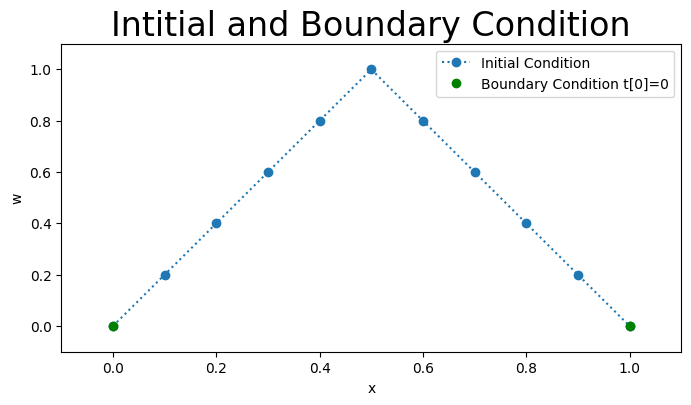
Discrete Initial and Boundary Conditions

The discrete initial conditions are

(607)\[\begin{equation} w[i,0]=2x[i], \ \ 0 \leq x[i] \leq \frac{1}{2} \end{equation}\]

(608)\[\begin{equation} w[i,0]=2(1-x[i]), \ \ \frac{1}{2} \leq x[i] \leq 1 \end{equation}\]

and the discete boundary conditions are

(609)\[\begin{equation} w[0,j]=0, w[10,j]=0, \end{equation}\]

where \(w[i,j]\) is the numerical approximation of \(U(x[i],t[j])\).

The Figure below plots values of \(w[i,0]\) for the inital (blue) and boundary (red) conditions for \(t[0]=0.\)

w=np.zeros((N+1,time_steps+1))
b=np.zeros(N-1)
# Initial Condition
for i in range (1,N):
    w[i,0]=2*x[i]
    if x[i]>0.5:
        w[i,0]=2*(1-x[i])
    

# Boundary Condition
for k in range (0,time_steps):
    w[0,k]=0
    w[N,k]=0

fig = plt.figure(figsize=(8,4))
plt.plot(x,w[:,0],'o:',label='Initial Condition')
plt.plot(x[[0,N]],w[[0,N],0],'go',label='Boundary Condition t[0]=0')
#plt.plot(x[N],w[N,0],'go')
plt.xlim([-0.1,1.1])
plt.ylim([-0.1,1.1])
plt.title('Intitial and Boundary Condition',fontsize=24)
plt.xlabel('x')
plt.ylabel('w')
plt.legend(loc='best')
plt.show()

The Implicit Crank-Nicolson Difference Equation

The implicit Crank-Nicolson difference equation of the Heat Equation is derived by discretising the

(610)\[\begin{equation} \frac{\partial u_{ij+\frac{1}{2}}}{\partial t} = \frac{\partial^2 u_{ij+\frac{1}{2}}}{\partial x^2},\end{equation}\]

around \((x_i,t_{j+\frac{1}{2}})\) giving the difference equation

(611)\[\begin{equation} \frac{w_{ij+1}-w_{ij}}{k}=\frac{1}{2}\left(\frac{w_{i+1j+1}-2w_{ij+1}+w_{i-1j+1}}{h^2}+\frac{w_{i+1j}-2w_{ij}+w_{i-1j}}{h^2}\right) \end{equation}\]

Rearranging the equation we get

(612)\[\begin{equation} -rw_{i-1j+1}+(2+2r)w_{ij+1}-rw_{i+1j+1}=rw_{i-1j}+(2-2r)w_{ij}+rw_{i+1j} \end{equation}\]

for \(i=1,...9\) where \(r=\frac{k}{h^2}\).

This gives the formula for the unknown term \(w_{ij+1}\) at the \((ij+1)\) mesh points in terms of \(x[i]\) along the jth time row.

Hence we can calculate the unknown pivotal values of \(w\) along the first row of \(j=1\) in terms of the known boundary conditions.

This can be written in matrix form

(613)\[\begin{equation} A\mathbf{w}_{j+1}=B\mathbf{w}_{j} +\mathbf{b}_{j}+\mathbf{b}_{j+1} \end{equation}\]

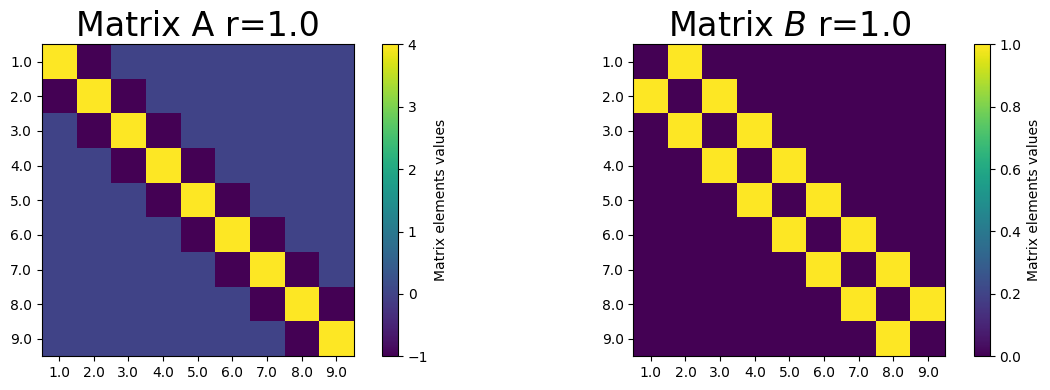
for which \(A\) is a \(9\times9\) matrix:

(614)\[\begin{equation} \left(\begin{array}{cccc cccc} 2+2r&-r& 0&0&0 &0&0&0\\ -r&2+2r&-r&0&0&0 &0&0&0\\ 0&-r&2+2r &-r&0&0& 0&0&0\\ 0&0&-r&2+2r &-r&0&0& 0&0\\ 0&0&0&-r&2+2r &-r&0&0& 0\\ 0&0&0&0&-r&2+2r &-r&0&0\\ 0&0&0&0&0&-r&2+2r &-r&0\\ 0&0&0&0&0&0&-r&2+2r&-r\\ 0&0&0&0&0&0&0&-r&2+2r\\ \end{array}\right) \left(\begin{array}{c} w_{1j+1}\\ w_{2j+1}\\ w_{3j+1}\\ w_{4j+1}\\ w_{5j+1}\\ w_{6j+1}\\ w_{7j+1}\\ w_{8j+1}\\ w_{9j+1}\\ \end{array}\right)= \left(\begin{array}{cccc cccc} 2-2r&r& 0&0&0 &0&0&0\\ r&2-2r&r&0&0&0 &0&0&0\\ 0&r&2-2r &r&0&0& 0&0&0\\ 0&0&r&2-2r &r&0&0& 0&0\\ 0&0&0&r&2-2r &r&0&0& 0\\ 0&0&0&0&r&2-2r &r&0&0\\ 0&0&0&0&0&r&2-2r &r&0\\ 0&0&0&0&0&0&r&2-2r&r\\ 0&0&0&0&0&0&0&r&2-2r\\ \end{array}\right) \left(\begin{array}{c} w_{1j}\\ w_{2j}\\ w_{3j}\\ w_{4j}\\ w_{5j}\\ w_{6j}\\ w_{7j}\\ w_{8j}\\ w_{9j}\\ \end{array}\right)+ \left(\begin{array}{c} rw_{0j}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ rw_{10j}\\ \end{array}\right)+ \left(\begin{array}{c} rw_{0j+1}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ rw_{10j+1}\\ \end{array}\right). \end{equation}\]

It is assumed that the boundary values \(w_{0j}\) and \(w_{10j}\) are known for \(j=1,2,...\), and \(w_{i0}\) for \(i=0,...,10\) is the initial condition.

The Figure below shows the values of the \(9\times 9\) matrix in colour plot form for \(r=\frac{k}{h^2}\).

A=np.zeros((N-1,N-1))
B=np.zeros((N-1,N-1))
for i in range (0,N-1):
    A[i,i]=2+2*r
    B[i,i]=2-2*r

for i in range (0,N-2):           
    A[i+1,i]=-r
    A[i,i+1]=-r
    B[i+1,i]=r
    B[i,i+1]=r
    
Ainv=np.linalg.inv(A)   
fig = plt.figure(figsize=(12,4));
plt.subplot(121)
plt.imshow(A,interpolation='none');
plt.xticks(np.arange(N-1), np.arange(1,N-0.9,1));
plt.yticks(np.arange(N-1), np.arange(1,N-0.9,1));
clb=plt.colorbar();
clb.set_label('Matrix elements values');
#clb.set_clim((-1,1));
plt.title('Matrix A r=%s'%(np.round(r,3)),fontsize=24)

plt.subplot(122)
plt.imshow(B,interpolation='none');
plt.xticks(np.arange(N-1), np.arange(1,N-0.9,1));
plt.yticks(np.arange(N-1), np.arange(1,N-0.9,1));
clb=plt.colorbar();
clb.set_label('Matrix elements values');
#clb.set_clim((-1,1));
plt.title(r'Matrix $B$ r=%s'%(np.round(r,3)),fontsize=24)
fig.tight_layout()
plt.show();

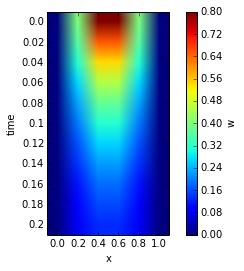
Results

To numerically approximate the solution at \(t[1]\) the matrix equation becomes

(615)\[\begin{equation} \mathbf{w}_{1}=A^{-1}(B\mathbf{w}_{0} +\mathbf{b}_{1}+\mathbf{b}_{0}) \end{equation}\]

where all the right hand side is known. To approximate solution at time \(t[2]\) we use the matrix equation

(616)\[\begin{equation}\mathbf{w}_{2}=A^{-1}(B\mathbf{w}_{1}+\mathbf{b}_{2} +\mathbf{b}_{1}). \end{equation}\]

Each set of numerical solutions \(w[i,j]\) for all \(i\) at the previous time step is used to approximate the solution \(w[i,j+1]\). The left and right plot below show the numerical approximation \(w[i,j]\) of the Heat Equation using the Crank-Nicolson method for \(x[i]\) for \(i=0,...,10\) and time steps \(t[j]\) for \(j=1,...,15\).

fig = plt.figure(figsize=(12,6))
plt.subplot(121)
for j in range (0,time_steps+1):
    b[0]=r*w[0,j-1]+r*w[0,j]
    b[N-2]=r*w[N,j-1]+r*w[N,j]
    v=np.dot(B,w[1:(N),j-1])
    w[1:(N),j]=np.dot(Ainv,v+b)
    plt.plot(x,w[:,j],'o:',label='t[%s]=%s'%(j,time[j]))
plt.xlabel('x')
plt.ylabel('w')
#plt.legend(loc='bottom', bbox_to_anchor=(0.5, -0.1))
plt.legend(bbox_to_anchor=(-.4, 1), loc=2, borderaxespad=0.)

plt.subplot(122)
plt.imshow(w.transpose())
plt.xticks(np.arange(len(x)), x)
plt.yticks(np.arange(len(time)), time)
plt.xlabel('x')
plt.ylabel('time')
clb=plt.colorbar()
clb.set_label('Temperature (w)')
plt.suptitle('Numerical Solution of the  Heat Equation r=%s'%(np.round(r,3)),fontsize=24,y=1.08)
fig.tight_layout()
plt.show()

Local Trunction Error

The local truncation error of the Crank-Nicoloson we approximate

(617)\[\begin{equation} \frac{\partial U}{\partial t} - \frac{\partial^2 U}{\partial x^2}=0, \end{equation}\]

with

(618)\[\begin{equation} F_{ij+\frac{1}{2}}(w)=\frac{w_{ij+1}-w_{ij}}{k}-\frac{1}{2}\left(\frac{w_{i+1j}-2w_{ij}+w_{i-1j}}{h^2} +\frac{w_{i+1j+1}-2w_{ij+1}+w_{i-1j+1}}{h^2} \right)=0.\end{equation}\]

Subbing the exact answer into the difference equation gives the truncation error

(619)\[\begin{equation} T_{ij+\frac{1}{2}}=F_{ij+\frac{1}{2}}(U)=\frac{U_{ij+1}-U_{ij}}{k}-\frac{1}{2}\left(\frac{U_{i+1j}-2U_{ij}+U_{i-1j}}{h^2}+\frac{U_{i+1j+1}-2U_{ij+1}+U_{i-1j+1}}{h^2}\right), \end{equation}\]

simplify

(620)\[\begin{equation} U_{ij+\frac{1}{2}}=\frac{U_{ij+1}+U_{ij}}{2}, \end{equation}\]

substitute into equation

(621)\[\begin{equation} T_{ij+\frac{1}{2}}=F_{ij+\frac{1}{2}}(U)=\frac{U_{ij+1}-U_{ij}}{k}-\frac{U_{i+1j+\frac{1}{2}}-2U_{ij+\frac{1}{2}}+U_{i-1j+\frac{1}{2}}}{h^2}, \end{equation}\]

By Taylors expansions we have

\[\begin{eqnarray*} U_{i+1j+\frac{1}{2}}&=&U((i+1)h,(j+\frac{1}{2})k)=U(x_i+h,t_j+\frac{1}{2}k)\\ &=&U_{ij+\frac{1}{2}}+h\left(\frac{\partial U}{\partial x} \right)_{ij+\frac{1}{2}}+\frac{h^2}{2}\left(\frac{\partial^2 U}{\partial x^2} \right)_{ij+\frac{1}{2}}+\frac{h^3}{6}\left(\frac{\partial^3 U}{\partial x^3} \right)_{ij+\frac{1}{2}} +...\\ U_{i-1j+\frac{1}{2}}&=&U((i-1)h,(j+\frac{1}{2})k)=U(x_i-h,t_j+\frac{1}{2}k)\\ &=&U_{ij+\frac{1}{2}}-h\left(\frac{\partial U}{\partial x} \right)_{ij+\frac{1}{2}}+\frac{h^2}{2}\left(\frac{\partial^2 U}{\partial x^2} \right)_{ij+\frac{1}{2}}-\frac{h^3}{6}\left(\frac{\partial^3 U}{\partial x^3} \right)_{ij+\frac{1}{2}} +...\\ U_{ij+1}&=&U(ih,(j+1)k)=U(x_i,t_j+k)\\ &=&U_{ij+\frac{1}{2}}+\frac{k}{2}\left(\frac{\partial U}{\partial t} \right)_{ij+\frac{1}{2}}+\frac{(\frac{k}{2})^2}{2}\left(\frac{\partial^2 U}{\partial t^2} \right)_{ij+\frac{1}{2}}+\frac{(\frac{k}{2})^3}{6}\left(\frac{\partial^3 U}{\partial t^3} \right)_{ij+\frac{1}{2}} +...\\ U_{ij-1}&=&U(ih,(j-1)k)=U(x_i,t_j-k)\\ &=&U_{ij+\frac{1}{2}}-\frac{k}{2}\left(\frac{\partial U}{\partial t} \right)_{ij+\frac{1}{2}}+\frac{(\frac{k}{2})^2}{2}\left(\frac{\partial^2 U}{\partial t^2} \right)_{ij+\frac{1}{2}}-\frac{(\frac{k}{2})^3}{6}\left(\frac{\partial^3 U}{\partial t^3} \right)_{ij+\frac{1}{2}} +... \end{eqnarray*}\]

substitution into the expression for \(T_{ij+\frac{1}{2}}\) then gives

\[\begin{eqnarray*} T_{ij+\frac{1}{2}}&=&\left(\frac{\partial U}{\partial t} - \frac{\partial^2 U}{\partial x^2} \right)_{ij+\frac{1}{2}} -\frac{h^2}{12}\left(\frac{\partial^4 U}{\partial x^4} \right)_{ij+\frac{1}{2}}\\ & & +\frac{k^2}{24}\left(\frac{\partial^3 U}{\partial t^3} \right)_{ij+\frac{1}{2}} -\frac{h^4}{360}\left(\frac{\partial^6 U}{\partial x^6} \right)_{ij+\frac{1}{2}}+ ... \end{eqnarray*}\]

But \(U\) is the solution to the differential equation so

(622)\[\begin{equation} \left(\frac{\partial U}{\partial t} - \frac{\partial^2 U}{\partial x^2} \right)_{ij+\frac{1}{2}}=0,\end{equation}\]

the principal part of the local truncation error is

(623)\[\begin{equation} \frac{k^2}{24}\left(\frac{\partial^3 U}{\partial t^3} \right)_{ij+\frac{1}{2}}-\frac{h^2}{12}\left(\frac{\partial^4 U}{\partial x^4} \right)_{ij+\frac{1}{2}}. \end{equation}\]

Hence the truncation error is

(624)\[\begin{equation} T_{ij}=O(k^2)+O(h^2). \end{equation}\]

Stability Analyis

To investigating the stability of the fully implicit Crank Nicolson difference method of the Heat Equation, we will use the von Neumann method. The difference equation is:

(625)\[\begin{equation}\frac{1}{k}(w_{pq+1}-w_{pq})=\frac{1}{2}\left(\frac{1}{h_x^2}(w_{p-1q+1}-2w_{pq+1}+w_{p+1q+1})+\frac{1}{h_x^2}(w_{p-1q}-2w_{pq}+w_{p+1q})\right),\end{equation}\]

approximating

(626)\[\begin{equation}\frac{\partial U}{\partial t}=\frac{\partial^2 U}{\partial x^2}\end{equation}\]

at \((ph,(q+\frac{1}{2})k)\). Substituting \(w_{pq}=e^{i\beta x}\xi^{q}\) into the difference equation gives:

(627)\[\begin{equation}e^{i\beta ph}\xi^{q+1}-e^{i\beta ph}\xi^{q}=\frac{1}{2}\left(r\{e^{i\beta (p-1)h}\xi^{q+1}-2e^{i\beta ph}\xi^{q+1}+e^{i\beta (p+1)h}\xi^{q+1}+e^{i\beta (p-1)h}\xi^{q}-2e^{i\beta ph}\xi^{q}+e^{i\beta (p+1)h}\xi^{q} \right) \} \end{equation}\]

where \(r=\frac{k}{h_x^2}\). Divide across by \(e^{i\beta (p)h}\xi^{q}\) leads to

(628)\[\begin{equation} \xi-1=r \xi (e^{i\beta (-1)h} -2+e^{i\beta h})+r (e^{i\beta (-1)h} -2+e^{i\beta h}), \end{equation}\]

(629)\[\begin{equation}\xi-\xi r (2\cos(\beta h)-2)= 1+r (2\cos(\beta h)-2),\end{equation}\]

(630)\[\begin{equation}\xi(1+4r\sin^2(\beta\frac{h}{2})) =1-4r\sin^2(\beta\frac{h}{2})\end{equation}\]

Hence

(631)\[\begin{equation}\xi=\frac{1-4r\sin^2(\beta\frac{h}{2})}{(1+4r\sin^2(\beta\frac{h}{2}))} \leq 1\end{equation}\]

therefore the equation is unconditionally stable as \(0 < \xi \leq 1\) for all \(r\) and all \(\beta\) .

References

[1] G D Smith Numerical Solution of Partial Differential Equations: Finite Difference Method Oxford 1992

[2] Butler, J. (2019). John S Butler Numerical Methods for Differential Equations. [online] Maths.dit.ie. Available at: http://www.maths.dit.ie/~johnbutler/Teaching_NumericalMethods.html [Accessed 14 Mar. 2019].

[3] Wikipedia contributors. (2019, February 22). Heat equation. In Wikipedia, The Free Encyclopedia. Available at: https://en.wikipedia.org/w/index.php?title=Heat_equation&oldid=884580138 [Accessed 14 Mar. 2019].