Problem Sheet 3 Question 7b

The general form of the population growth differential equation

(177)\[\begin{equation} y^{'}-y+x=0, \ \ (0 \leq x \leq 1) \end{equation}\]

with the initial condition

(178)\[\begin{equation}y(0)=0\end{equation}\]

For h=0.2.

Midpoint method Solution

(179)\[\begin{equation} \frac{w_{i+1}-w_i}{h}=f(x_i+\frac{h}{2},w_i+\frac{h}{2}f(x_i,w_i)) \end{equation}\]

Rearranging

(180)\[\begin{equation} w_{i+1}=w_i+hf(x_i+\frac{h}{2},w_i+\frac{h}{2}f(x_i,w_i)) \end{equation}\]

(181)\[\begin{equation} w_{i+1}=w_i+h(k_2) \end{equation}\]

(182)\[\begin{equation} k_1=w_i-x_i+2 \end{equation}\]

(183)\[\begin{equation} k_2=w_i+\frac{h}{2}k_1-(x_i+\frac{h}{2})+2) \end{equation}\]

import numpy as np
import math 
%matplotlib inline
import matplotlib.pyplot as plt # side-stepping mpl backend
import matplotlib.gridspec as gridspec # subplots
import warnings
warnings.filterwarnings("ignore")

def myfun_xy(x,y):
    return y-x+2

#PLOTS
def Midpoint_Question2(N,IC):

    x_start=0
    INTITIAL_CONDITION=IC
    h=0.2
    N=N+1
    x=np.zeros(N)
    w=np.zeros(N)
    k_mat=np.zeros((2,N))
    k=0
    w[0]=INTITIAL_CONDITION
    x[0]=x_start
    
    for k in range (0,N-1):
        k_mat[0,k]=myfun_xy(x[k],w[k])
        k_mat[1,k]=myfun_xy(x[k]+h/2,w[k]+h/2*k_mat[0,k])
        w[k+1]=w[k]+h*(k_mat[1,k])
        x[k+1]=x[k]+h


    fig = plt.figure(figsize=(10,4))
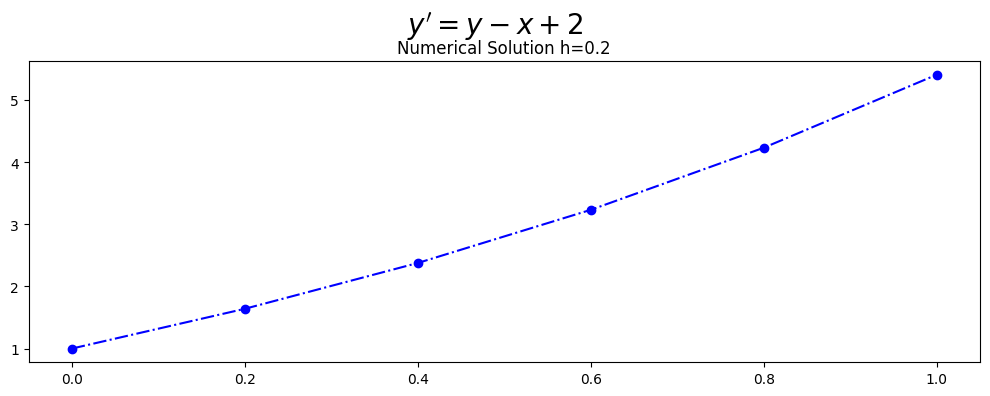
    plt.plot(x,w,'-.o',color='blue')
    plt.title('Numerical Solution h=%s'%(h))

    # --- title, explanatory text and save
    fig.suptitle(r"$y'=y-x+2$", fontsize=20)
    plt.tight_layout()
    plt.subplots_adjust(top=0.85)    
    print('x')
    print(x)
    print('k1')
    print(k_mat[0,:])
    print('k2')
    print(k_mat[1,:])
    print('w')
    print(w)

# Midpoint_Question2(N,IC)
Midpoint_Question2(5,1)

x
[0.  0.2 0.4 0.6 0.8 1. ]
k1
[3.         3.44       3.9768     4.631696   5.43066912 0.        ]
k2
[3.2        3.684      4.27448    4.9948656  5.87373603 0.        ]
w
[1.         1.64       2.3768     3.231696   4.23066912 5.40541633]