Adams Bashforth

John S Butler

john.s.butler@tudublin.ie
Course Notes Github

The Adams Bashforth method is an explicit multistep method. This notebook illustrates the 2 step Adams Bashforth method for a linear initial value problem, given by

(184)\[\begin{equation}y^{'}=t-y, \ \ (0 \leq t \leq 2) \end{equation}\]

with the initial condition

(185)\[\begin{equation}y(0)=1.\end{equation}\]

The video below walks through the notebook.

from IPython.display import HTML
HTML('<iframe width="560" height="315" src="https://www.youtube.com/embed/etob5sngUUc" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>')

/Users/johnbutler/opt/anaconda3/lib/python3.8/site-packages/IPython/core/display.py:724: UserWarning: Consider using IPython.display.IFrame instead
  warnings.warn("Consider using IPython.display.IFrame instead")

Python Libraries

import numpy as np
import math 
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt # side-stepping mpl backend
import matplotlib.gridspec as gridspec # subplots
import warnings

warnings.filterwarnings("ignore")

Defining the function

(186)\[\begin{equation} f(t,y)=t-y.\end{equation}\]

def myfun_ty(t,y):
    return t-y

Discrete Interval

Defining the step size \(h\) from the interval range \(a\leq t \leq b\) and number of steps \(N\)

(187)\[\begin{equation}h=\frac{b−a}{N}.\end{equation}\]

This gives the discrete time steps,

(188)\[\begin{equation}t_i=t_0+ih,\end{equation}\]

where \(t0=a.\)

Here the interval is \(0≤t≤2\) and number of step 4

(189)\[\begin{equation}h=\frac{2−0}{4}=0.5.\end{equation}\]

This gives the discrete time steps,

(190)\[\begin{equation}t_i=0+i0.5,\end{equation}\]

for \(i=0,1,⋯,4.\)

# Start and end of interval
b=2
a=0
# Step size
N=4
h=(b-a)/(N)
t=np.arange(a,b+h,h)
fig = plt.figure(figsize=(10,4))
plt.plot(t,0*t,'o:',color='red')
plt.xlim((0,2))
plt.title('Illustration of discrete time points for h=%s'%(h))

Text(0.5, 1.0, 'Illustration of discrete time points for h=0.5')

Exact Solution

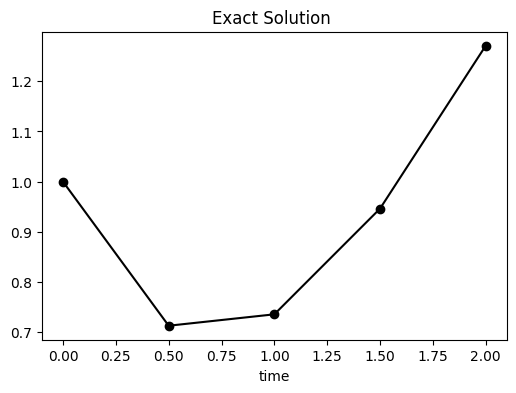
THe initial value problem has the exact solution

(191)\[\begin{equation}y(t)=2e^{-t}+t-1.\end{equation}\]

The figure below plots the exact solution.

IC=1 # Intial condtion
y=(IC+1)*np.exp(-t)+t-1
fig = plt.figure(figsize=(6,4))
plt.plot(t,y,'o-',color='black')
plt.title('Exact Solution ')
plt.xlabel('time')

Text(0.5, 0, 'time')

2-step Adams Bashforth

The general 2-step Adams Bashforth difference equation is

(192)\[\begin{equation}w_{i+1} = w_{i} + \frac{h}{2}(3f(t_i,w_i)-f(t_{i-1},w_{i-1})). \end{equation}\]

For the specific intial value problem the 2-step Adams Bashforth difference equation is

(193)\[\begin{equation}w_{i+1} = w_{i} + \frac{h}{2}(3(t_i-w_i)-(t_{i-1}-w_{i-1})). \end{equation}\]

for \(i=0\) the difference equation is:

(194)\[\begin{equation}w_{1} = w_{0} + \frac{h}{2}(3(t_0-w_0)-(t_{-1}-w_{-1})), \end{equation}\]

this is not solvable as \(w_{-1}\) is unknown. for \(i=1\) the difference equation is:

(195)\[\begin{equation}w_{2} = w_{1} + \frac{h}{2}(3(t_1-w_1)-(t_{0}-w_{0})), \end{equation}\]

this is not solvable as \(w_{1}\) is unknown, but it can be approximated using a one step method. Here, as the exact solution is known,

(196)\[\begin{equation}w_1=2e^{-t_1}+t_1-1.\end{equation}\]

### Initial conditions
w=np.zeros(len(t))
w[0]=IC
w[1]=y[1] # NEED FOR THE METHOD

Loop

for k in range (1,N):
    w[k+1]=w[k]+h/2.0*(3*myfun_ty(t[k],w[k])-myfun_ty(t[k-1],w[k-1]))   

Plotting solution

def plotting(t,w,y):
    fig = plt.figure(figsize=(10,4))
    plt.plot(t,y, 'o-',color='black',label='Exact')
    plt.plot(t,w,'s:',color='blue',label='Adams-Bashforth')
    plt.xlabel('time')
    plt.legend()
    plt.show 

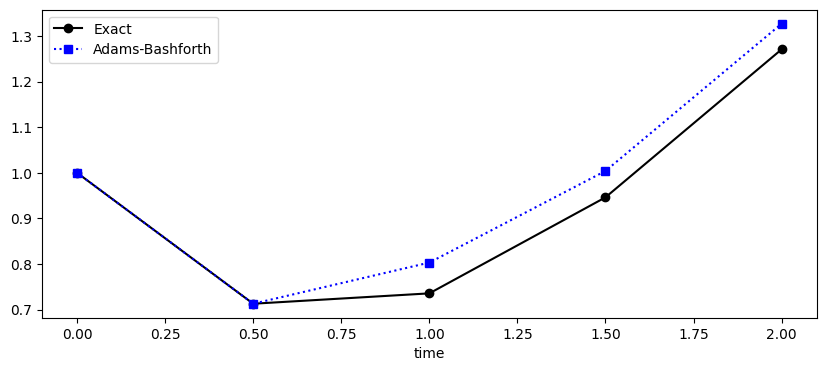
The plot below shows the exact solution (black) and the 2 step Adams-Bashforth approximation (red) of the intial value problem

plotting(t,w,y)

Local Error

The Error for the 2 step Adams Bashforth is:

(197)\[\begin{equation}y_{n+1}=y_n+\frac{h}{2}[3f(t_{n},w_{n})-f(t_{n-1},w_{n-1})] +\frac{5h^3}{12}y'''(\eta),\end{equation}\]

where \(\eta \in [t_{n-1},t_{n+1}]\).

Rearranging the equations gives

(198)\[\begin{equation}\frac{y_{n+1}-y_n}{h}=\frac{1}{2}[3f(t_{n},w_{n})-f(t_{n-1},w_{n-1})] +\frac{5h^2}{12}y'''(\eta).\end{equation}\]

For our specific initial value problem the error is of the form:

(199)\[\begin{equation}\frac{5h^2}{12}y'''(\eta)=\frac{5h^2}{12}2e^{-\eta} \leq\frac{5(0.5)^2}{12} 2\leq 0.208 \end{equation}\]

d = {'time t_i': t, 'Adams Bashforth, w_i': w,'Exact':y,'Error |w-y|':np.round(np.abs(y-w),5),'LTE':round(2*0.5**2/12*5,5)}
df = pd.DataFrame(data=d)
df

	time t_i	Adams Bashforth, w_i	Exact	Error |w-y|	LTE
0	0.0	1.000000	1.000000	0.00000	0.20833
1	0.5	0.713061	0.713061	0.00000	0.20833
2	1.0	0.803265	0.735759	0.06751	0.20833
3	1.5	1.004082	0.946260	0.05782	0.20833
4	2.0	1.326837	1.270671	0.05617	0.20833