The Explicit Forward Time Centered Space (FTCS) Difference Equation for the Heat Equation

The Explicit Forward Time Centered Space (FTCS) Difference Equation for the Heat Equation#

John S Butler john.s.butler@tudublin.ie Course Notes Github #

Overview#

This notebook will implement the explicit Forward Time Centered Space (FTCS) Difference method for the Heat Equation.

The Heat Equation#

The Heat Equation is the first order in time ($t$) and second order in space ($x$) Partial Differential Equation [1-3]: $$ \frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2},$$ The equation describes heat transfer on a domain $$ \Omega = \{ t \geq 0\leq x \leq 1\}. $$ with an initial condition at time $t=0$ for all $x$ and boundary condition on the left ($x=0$) and right side ($x=1$).

Forward Time Centered Space (FTCS) Difference method#

This notebook will illustrate the Forward Time Centered Space (FTCS) Difference method for the Heat Equation with the initial conditions
$$ u(x,0)=2x, \ \ 0 \leq x \leq \frac{1}{2}, $$ u(x,0)=2(1-x), \ \ \frac{1}{2} \leq x \leq 1, $$ and __boundary condition__ $$ u(0,t)=0, u(1,t)=0. $$

# LIBRARY
# vector manipulation
import numpy as np
# math functions
import math 
import jupytext
# THIS IS FOR PLOTTING
%matplotlib inline
import matplotlib.pyplot as plt # side-stepping mpl backend
import warnings
warnings.filterwarnings("ignore")

Discete Grid#

The region $\Omega$ is discretised into a uniform mesh $\Omega_h$. In the space $x$ direction into $N$ steps giving a stepsize of $$ h=\frac{1-0}{N},$$ resulting in $$x[i]=0+ih, \ \ \ i=0,1,...,N,$$ and into $N_t$ steps in the time $t$ direction giving a stepsize of $$ k=\frac{1-0}{N_t}$$ resulting in $$t[j]=0+jk, \ \ \ j=0,...,15.$$ The Figure below shows the discrete grid points for $N=10$ and $Nt=100$, the known boundary conditions (green), initial conditions (blue) and the unknown values (red) of the Heat Equation.

N=10
Nt=1000
h=1/N
k=1/Nt
r=k/(h*h)
time_steps=15
time=np.arange(0,(time_steps+.5)*k,k)
x=np.arange(0,1.0001,h)
X, Y = np.meshgrid(x, time)
fig = plt.figure()
plt.plot(X,Y,'ro');
plt.plot(x,0*x,'bo',label='Initial Condition');
plt.plot(np.ones(time_steps+1),time,'go',label='Boundary Condition');
plt.plot(x,0*x,'bo');
plt.plot(0*time,time,'go');
plt.xlim((-0.02,1.02))
plt.xlabel('x')
plt.ylabel('time (ms)')
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.title(r'Discrete Grid $\Omega_h,$ h= %s, k=%s'%(h,k),fontsize=24,y=1.08)
plt.show();

Discrete Initial and Boundary Conditions#

The discrete initial conditions are $$ w[i,0]=2x[i], \ \ 0 \leq x[i] \leq \frac{1}{2} $$ w[i,0]=2(1-x[i]), \ \ \frac{1}{2} \leq x[i] \leq 1 $$ and the discrete boundary conditions are $$ w[0,j]=0, w[10,j]=0, $$ where $w[i,j]$ is the numerical approximation of $U(x[i],t[j])$.

The Figure below plots values of $w[i,0]$ for the inital (blue) and boundary (red) conditions for $t[0]=0.$

w=np.zeros((N+1,time_steps+1))
b=np.zeros(N-1)
# Initial Condition
for i in range (1,N):
    w[i,0]=2*x[i]
    if x[i]>0.5:
        w[i,0]=2*(1-x[i])
    

# Boundary Condition
for k in range (0,time_steps):
    w[0,k]=0
    w[N,k]=0

fig = plt.figure(figsize=(8,4))
plt.plot(x,w[:,0],'o:',label='Initial Condition')
plt.plot(x[[0,N]],w[[0,N],0],'go',label='Boundary Condition t[0]=0')
#plt.plot(x[N],w[N,0],'go')
plt.xlim([-0.1,1.1])
plt.ylim([-0.1,1.1])
plt.title('Intitial and Boundary Condition',fontsize=24)
plt.xlabel('x')
plt.ylabel('w')
plt.legend(loc='best')
plt.show()

The Explicit Forward Time Centered Space (FTCS) Difference Equation#

The explicit Forwards Time Centered Space (FTCS) difference equation of the Heat Equation is derived by discretising $$ \frac{\partial u_{ij}}{\partial t} = \frac{\partial^2 u_{ij}}{\partial x^2},$$ around $(x_i,t_{j})$ giving the difference equation $$ \frac{w_{ij+1}-w_{ij}}{k}=\frac{w_{i+1j}-2w_{ij}+w_{i-1j}}{h^2}, $$ Rearranging the equation we get $$ w_{ij+1}=rw_{i-1j}+(1-2r)w_{ij}+rw_{i+1j}, $$ for $i=1,…9$ where $r=\frac{k}{h^2}$.

This gives the formula for the unknown term $w_{ij+1}$ at the $(ij+1)$ mesh points in terms of $x[i]$ along the jth time row.

Hence we can calculate the unknown pivotal values of $w$ along the first row of $j=1$ in terms of the known boundary conditions.

This can be written in matrix form $$ \mathbf{w}_{j+1}=A\mathbf{w}_{j} +\mathbf{b}_{j} $$ for which $A$ is a $9\times9$ matrix: $$ \left(\begin{array}{c} w_{1j+1}\\ w_{2j+1}\\ w_{3j+1}\\ w_{4j+1}\\ w_{5j+1}\\ w_{6j+1}\\ w_{7j+1}\\ w_{8j+1}\\ w_{9j+1}\\ \end{array}\right). =\left(\begin{array}{cccc cccc} 1-2r&r& 0&0&0 &0&0&0\\ r&1-2r&r&0&0&0 &0&0&0\\ 0&r&1-2r &r&0&0& 0&0&0\\ 0&0&r&1-2r &r&0&0& 0&0\\ 0&0&0&r&1-2r &r&0&0& 0\\ 0&0&0&0&r&1-2r &r&0&0\\ 0&0&0&0&0&r&1-2r &r&0\\ 0&0&0&0&0&0&r&1-2r&r\\ 0&0&0&0&0&0&0&r&1-2r\\ \end{array}\right) \left(\begin{array}{c} w_{1j}\\ w_{2j}\\ w_{3j}\\ w_{4j}\\ w_{5j}\\ w_{6j}\\ w_{7j}\\ w_{8j}\\ w_{9j}\\ \end{array}\right)+ \left(\begin{array}{c} rw_{0j}\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ rw_{10j}\\ \end{array}\right). $$ It is assumed that the boundary values $w_{0j}$ and $w_{10j}$ are known for $j=1,2,…$, and $w_{i0}$ for $i=0,…,10$ is the initial condition.

The Figure below shows the values of the $9\times 9$ matrix in colour plot form for $r=\frac{k}{h^2}$.

A=np.zeros((N-1,N-1))
for i in range (0,N-1):
    A[i,i]=1-2*r # DIAGONAL

for i in range (0,N-2):           
    A[i+1,i]=r # UPPER DIAGONAL
    A[i,i+1]=r # LOWER DIAGONAL
    
fig = plt.figure(figsize=(6,4));
#plt.matshow(A);
plt.imshow(A,interpolation='none');
plt.xticks(np.arange(N-1), np.arange(1,N-0.9,1));
plt.yticks(np.arange(N-1), np.arange(1,N-0.9,1));
clb=plt.colorbar();
clb.set_label('Matrix elements values');
#clb.set_clim((-1,1));
plt.title('Matrix r=%s'%(np.round(r,3)),fontsize=24)
fig.tight_layout()
plt.show();

Results#

To numerically approximate the solution at $t[1]$ the matrix equation becomes $$ \mathbf{w}_{1}=A\mathbf{w}_{0} +\mathbf{b}_{0} $$ where all the right hand side is known. To approximate solution at time $t[2]$ we use the matrix equation $$ \mathbf{w}_{2}=A\mathbf{w}_{1} +\mathbf{b}_{1}. $$ Each set of numerical solutions $w[i,j]$ for all $i$ at the previous time step is used to approximate the solution $w[i,j+1]$.

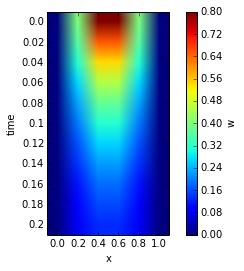
The Figure below shows the numerical approximation $w[i,j]$ of the Heat Equation using the FTCS method at $x[i]$ for $i=0,...,10$ and time steps $t[j]$ for $j=1,...,15$. The left plot shows the numerical approximation $w[i,j]$ as a function of $x[i]$ with each color representing the different time steps $t[j]$. The right plot shows the numerical approximation $w[i,j]$ as colour plot as a function of $x[i]$, on the $x[i]$ axis and time $t[j]$ on the $y$ axis.

For $r>\frac{1}{2}$ the method is unstable resulting a solution that oscillates unnaturally between positive and negative values for each time step.

fig = plt.figure(figsize=(12,6))

plt.subplot(121)
for j in range (1,time_steps+1):
    b[0]=r*w[0,j-1]
    b[N-2]=r*w[N,j-1]
    w[1:(N),j]=np.dot(A,w[1:(N),j-1])
    plt.plot(x,w[:,j],'o:',label='t[%s]=%s'%(j,np.round(time[j],4)))
plt.xlabel('x')
plt.ylabel('w')
#plt.legend(loc='bottom', bbox_to_anchor=(0.5, -0.1))
plt.legend(bbox_to_anchor=(-.4, 1), loc=2, borderaxespad=0.)

plt.subplot(122)
plt.imshow(w.transpose())
plt.xticks(np.arange(len(x)), x)
plt.yticks(np.arange(len(time)), np.round(time,4))
plt.xlabel('x')
plt.ylabel('time')
clb=plt.colorbar()
clb.set_label('Temperature (w)')
plt.suptitle('Numerical Solution of the  Heat Equation r=%s'%(np.round(r,3)),fontsize=24,y=1.08)
fig.tight_layout()
plt.show()

Local Trunction Error#

The local truncation error of the classical explicit difference approach to

(557)#\[\begin{equation} \frac{\partial U}{\partial t} - \frac{\partial^2 U}{\partial x^2}=0, \end{equation}\]

with

(558)#\[\begin{equation} F_{ij}(w)=\frac{w_{ij+1}-w_{ij}}{k}-\frac{w_{i+1j}-2w_{ij}+w_{i-1j}}{h^2}=0, \end{equation}\]

is

(559)#\[\begin{equation} T_{ij}=F_{ij}(U)=\frac{U_{ij+1}-U_{ij}}{k}-\frac{U_{i+1j}-2U_{ij}+U_{i-1j}}{h^2}, \end{equation}\]

By Taylors expansions we have

\[\begin{eqnarray*} U_{i+1j}&=&U((i+1)h,jk)=U(x_i+h,t_j)\\ &=&U_{ij}+h\left(\frac{\partial U}{\partial x} \right)_{ij}+\frac{h^2}{2}\left(\frac{\partial^2 U}{\partial x^2} \right)_{ij}+\frac{h^3}{6}\left(\frac{\partial^3 U}{\partial x^3} \right)_{ij} +...\\ U_{i-1j}&=&U((i-1)h,jk)=U(x_i-h,t_j)\\ &=&U_{ij}-h\left(\frac{\partial U}{\partial x} \right)_{ij}+\frac{h^2}{2}\left(\frac{\partial^2 U}{\partial x^2} \right)_{ij}-\frac{h^3}{6}\left(\frac{\partial^3 U}{\partial x^3} \right)_{ij} +...\\ U_{ij+1}&=&U(ih,(j+1)k)=U(x_i,t_j+k)\\ &=&U_{ij}+k\left(\frac{\partial U}{\partial t} \right)_{ij}+\frac{k^2}{2}\left(\frac{\partial^2 U}{\partial t^2} \right)_{ij}+\frac{k^3}{6}\left(\frac{\partial^3 U}{\partial t^3} \right)_{ij} +... \end{eqnarray*}\]

substitution into the expression for $T_{ij}$ then gives

\[\begin{eqnarray*} T_{ij}&=&\left(\frac{\partial U}{\partial t} - \frac{\partial^2 U}{\partial x^2} \right)_{ij}+\frac{k}{2}\left(\frac{\partial^2 U}{\partial t^2} \right)_{ij} -\frac{h^2}{12}\left(\frac{\partial^4 U}{\partial x^4} \right)_{ij}\\ & & +\frac{k^2}{6}\left(\frac{\partial^3 U}{\partial t^3} \right)_{ij} -\frac{h^4}{360}\left(\frac{\partial^6 U}{\partial x^6} \right)_{ij}+ ... \end{eqnarray*}\]

But $U$ is the solution to the differential equation so

(560)#\[\begin{equation} \left(\frac{\partial U}{\partial t} - \frac{\partial^2 U}{\partial x^2} \right)_{ij}=0,\end{equation}\]

the principal part of the local truncation error is

(561)#\[\begin{equation} \frac{k}{2}\left(\frac{\partial^2 U}{\partial t^2} \right)_{ij}-\frac{h^2}{12}\left(\frac{\partial^4 U}{\partial x^4} \right)_{ij}. \end{equation}\]

Hence the truncation error is

(562)#\[\begin{equation} T_{ij}=O(k)+O(h^2). \end{equation}\]

Stability Analysis#

To investigating the stability of the fully explicit FTCS difference method of the Heat Equation, we will use the von Neumann method. The FTCS difference equation is: $$\frac{1}{k}(w_{pq+1}-w_{pq})=\frac{1}{h_x^2}(w_{p-1q}-2w_{pq}+w_{p+1q}),$$ approximating $$\frac{\partial U}{\partial t}=\frac{\partial^2 U}{\partial x^2}$$

at $(ph,qk)$. Substituting $w_{pq}=e^{i\beta x}\xi^{q}$ into the difference equation gives: $$e^{i\beta ph}\xi^{q+1}-e^{i\beta ph}\xi^{q}=r\{e^{i\beta (p-1)h}\xi^{q}-2e^{i\beta ph}\xi^{q}+e^{i\beta (p+1)h}\xi^{q} \} $$

where $r=\frac{k}{h_x^2}$. Divide across by $e^{i\beta (p)h}\xi^{q}$ leads to

\[ \xi-1=r(e^{i\beta (-1)h} -2+e^{i\beta h}), \]

\[\xi= 1+r (2\cos(\beta h)-2),\]

\[\xi=1-4r(\sin^2(\beta\frac{h}{2})).\]

Hence $$\left| 1-4r(\sin^2(\beta\frac{h}{2}) )\right|\leq 1$$ for this to hold $$ 4r(\sin^2(\beta\frac{h}{2}) )\leq 2 $$ which means $$ r\leq \frac{1}{2}. $$ therefore the equation is conditionally stable as $0 < \xi \leq 1$ for $r<\frac{1}{2}$ and all $\beta$ .

References#

[1] G D Smith Numerical Solution of Partial Differential Equations: Finite Difference Method Oxford 1992

[2] Butler, J. (2019). John S Butler Numerical Methods for Differential Equations. [online] Maths.dit.ie. Available at: http://www.maths.dit.ie/~johnbutler/Teaching_NumericalMethods.html [Accessed 14 Mar. 2019].

[3] Wikipedia contributors. (2019, February 22). Heat equation. In Wikipedia, The Free Encyclopedia. Available at: https://en.wikipedia.org/w/index.php?title=Heat_equation&oldid=884580138 [Accessed 14 Mar. 2019].