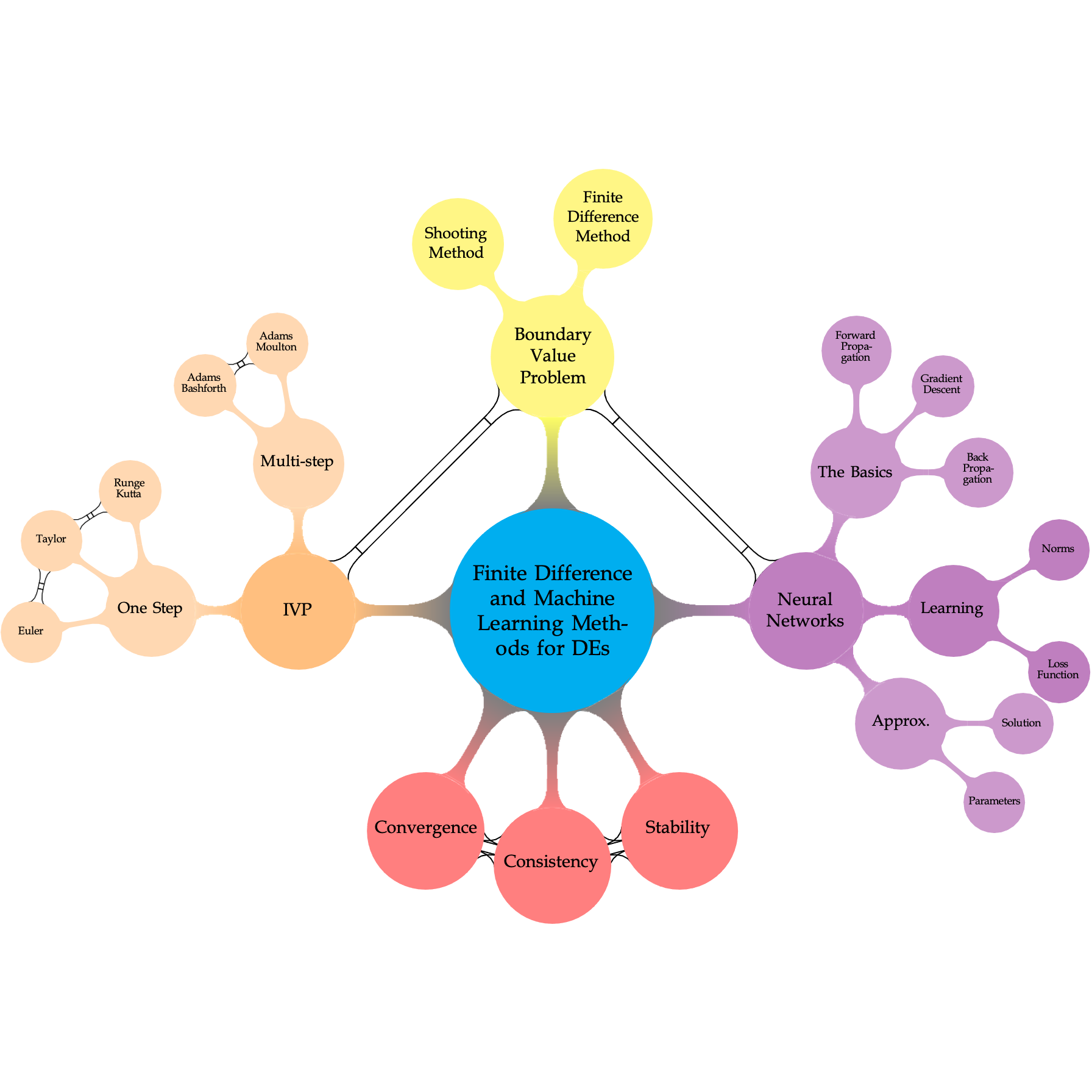
Comparison of Numerical Methods and ANNs#
Numerical Methods:
Principles:
Discretization: Classical methods, such as Euler’s method, Runge-Kutta methods, and finite difference methods, discretize the ODE by dividing the domain into smaller steps.
Local Approximation: These methods use local information about the solution to approximate the next value based on the current state.
Characteristics:
Accuracy and Stability: The accuracy of classical methods depends on the step size chosen, with smaller steps generally leading to more accurate solutions. Stability concerns may arise for stiff ODEs, requiring careful selection of methods and step sizes.
Deterministic: Classical methods provide deterministic results based on the initial conditions and the chosen algorithm.
Strengths:
Widespread Applicability: Classical methods are versatile and applicable to a wide range of ODEs.
Transparent: The solutions obtained are often interpretable and can be analyzed step by step.
Weaknesses:
Limited to Well-posed Problems: Classical methods may struggle with ill-posed or stiff ODEs.
Manual Tuning: Selecting an appropriate step size can be challenging and may require manual tuning.
Suitability:
Well-suited for: Problems with known properties, not excessively stiff ODEs, and situations where interpretability of the solution is crucial.
Artificial Neural Networks:
Principles:
Data-Driven Learning: ANNs learn from data, mapping input-output relationships without explicit knowledge of the underlying ODE.
Nonlinear Function Approximation: ANNs can capture complex, nonlinear relationships inherent in some ODEs.
Characteristics:
Adaptability: ANNs can adapt to different types of ODEs without needing explicit modifications.
Parallel Processing: ANNs can process information in parallel, potentially leading to faster solutions for certain problems.
Strengths:
Universal Approximators: ANNs can approximate any continuous function, making them powerful for solving ODEs with complex dynamics.
Robustness: ANNs can handle noisy data and adapt to changing conditions.
Weaknesses:
Lack of Transparency: The “black-box” nature of ANNs can make it challenging to interpret the learned solution.
Data Dependency: ANNs require sufficient high-quality data for training, which may not always be available.
Suitability:
Well-suited for: Complex, nonlinear ODEs where the underlying dynamics are not well-understood, and where large datasets are available for training.
In summary, classical numerical methods are reliable and interpretable but may struggle with certain types of ODEs. ANNs, on the other hand, excel in handling complex, nonlinear dynamics but may lack transparency and require substantial amounts of data for training. The choice between these methods depends on the specific characteristics of the problem at hand, such as the nature of the ODE, the availability of data, and the desired level of interpretability.