Activation Functions

import numpy as np
import matplotlib.pyplot as plt
# Plotting the Activation Functions
x = np.linspace(-10, 10,1000)

Activation functions are an essential component of neural networks. They introduce non-linearity in an inherently linear model, which is necessary for the network to learn complex patterns in the data. The derivative of activation functions is fundamental to the optimization of neural networks. In this article, we will discuss the commonly used activation functions in neural networks.

1. Linear Function: The linear function is just the line:

\[a(x)=wx+b, \]

with the derivative

\[a'(x)=w. \]

# Linear Activation Function
def linear(x):
    ''' y = f(x) It returns the input as it is'''
    w=1
    b=0
    return w*x+b
# Linear Activation Function Derivative
def dlinear(x):
    ''' y = f(x) It returns the input as it is'''
    w=1
    b=0
    return w*np.ones(len(x))

plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(x, linear(x), )
plt.title('Linear Activation Function')
plt.subplot(1, 2, 2)

plt.plot(x, dlinear(x), label='Linear')
plt.title('Linear Activation Function Derivative')
plt.show()

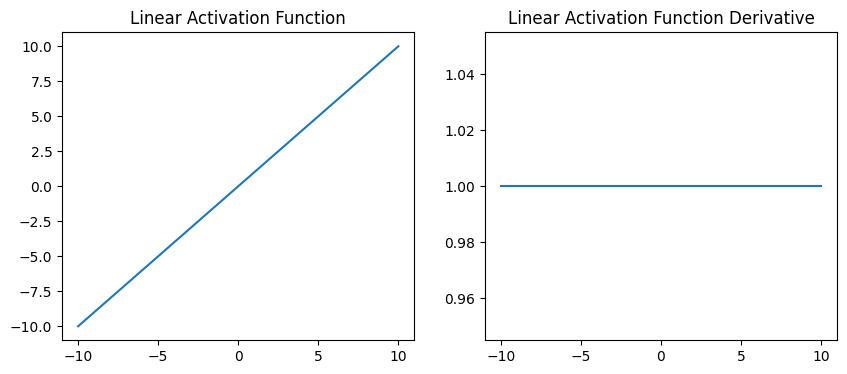
2. ReLU (Rectified Linear Unit) Function: The ReLU function is the most commonly used activation function in neural networks. It returns 0 for negative inputs and the input value for positive inputs. The ReLU function is computationally efficient and has been shown to work well in practice.

\[a(x)=max(0,wx+b), \]

with the derivative

\[a'(x)=w. \]

# ReLU Activation Function
def relu(x):
    w=1
    b=0
    return np.maximum(0, w*x+b)


# ReLU Activation Function Derivative
def drelu(x):
    w=1
    b=0
    dr=np.zeros(len(x));
    for i in range(0,len(x)):
        if w*x[i]+b>0:
             dr[i]=w
     
    return dr

plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(x, relu(x), )
plt.title('ReLU Activation Function')
plt.subplot(1, 2, 2)

plt.plot(x, drelu(x), label='Linear')
plt.title('ReLU Activation Function Derivative')
plt.show()

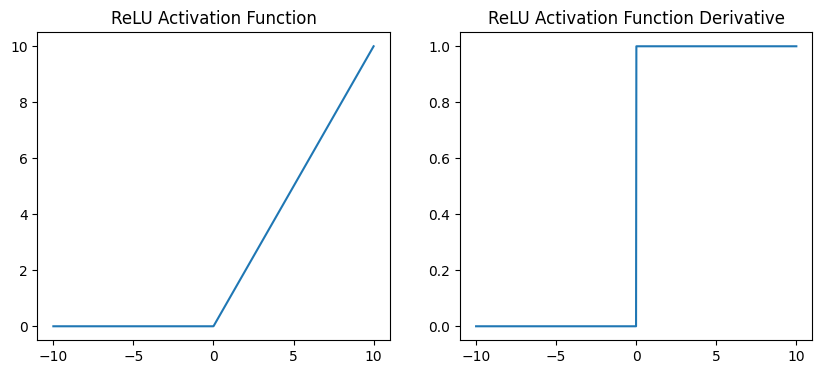
3. Sigmoid Function: The sigmoid function returns values between 0 and 1, given by the function:

\[\sigma(x)=\frac{1}{1+exp(-wx+b)}, \]

with the derivative

\[\sigma'(x)=\sigma(x)(1-\sigma(x)). \]

# Logistic Activation Function
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# Logistic Activation Function Derivative
def dsigmoid(x):
    return sigmoid(x)*(1-sigmoid(x))

plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(x, sigmoid(x), )
plt.title('Logistic Activation Function')
plt.subplot(1, 2, 2)

plt.plot(x, dsigmoid(x))
plt.title('Logistic Activation Function Derivative')
plt.show()

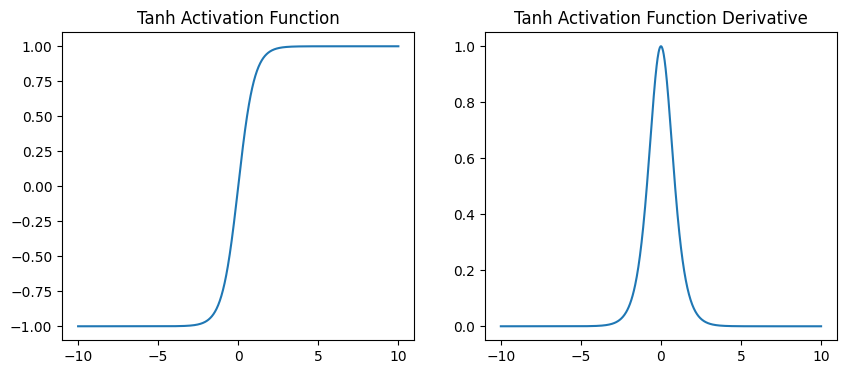
4. Tanh (Hyperbolic Tangent) Function: The tanh function returns values between -1 and 1 given by the function:

\[\tanh(x)=\frac{exp(wx+b)-exp(wx+b)}{exp(wx+b)-exp(wx+b)} \]

with the derivative

\[\tanh'(x)=1-\tanh^2(wx+b). \]

# Tanh Activation Function
def tanh(x):
    w=1
    b=0
    return np.tanh(w*x+b)

# Tanh Activation Function Derivative
def dtanh(x):
    return 1-np.tanh(x)*np.tanh(x)

plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
plt.plot(x, tanh(x), )
plt.title('Tanh Activation Function')
plt.subplot(1, 2, 2)

plt.plot(x, dtanh(x))
plt.title('Tanh Activation Function Derivative')
plt.show()

The choice of activation function depends on the problem at hand and the architecture of the neural network.

Other Activation Functions

5. Leaky ReLU Function: The Leaky ReLU function is a variant of the ReLU function that returns a small negative value for negative inputs. It has been shown to work well in practice for deep neural networks.

6. ELU (Exponential Linear Unit) Function: The ELU function is a variant of the ReLU function that returns a small negative value for negative inputs. It has been shown to work well in practice for deep neural networks.

7. Softmax Function: The softmax function is commonly used in the output layer of neural networks for multi-class classification problems. It returns a probability distribution over the classes.