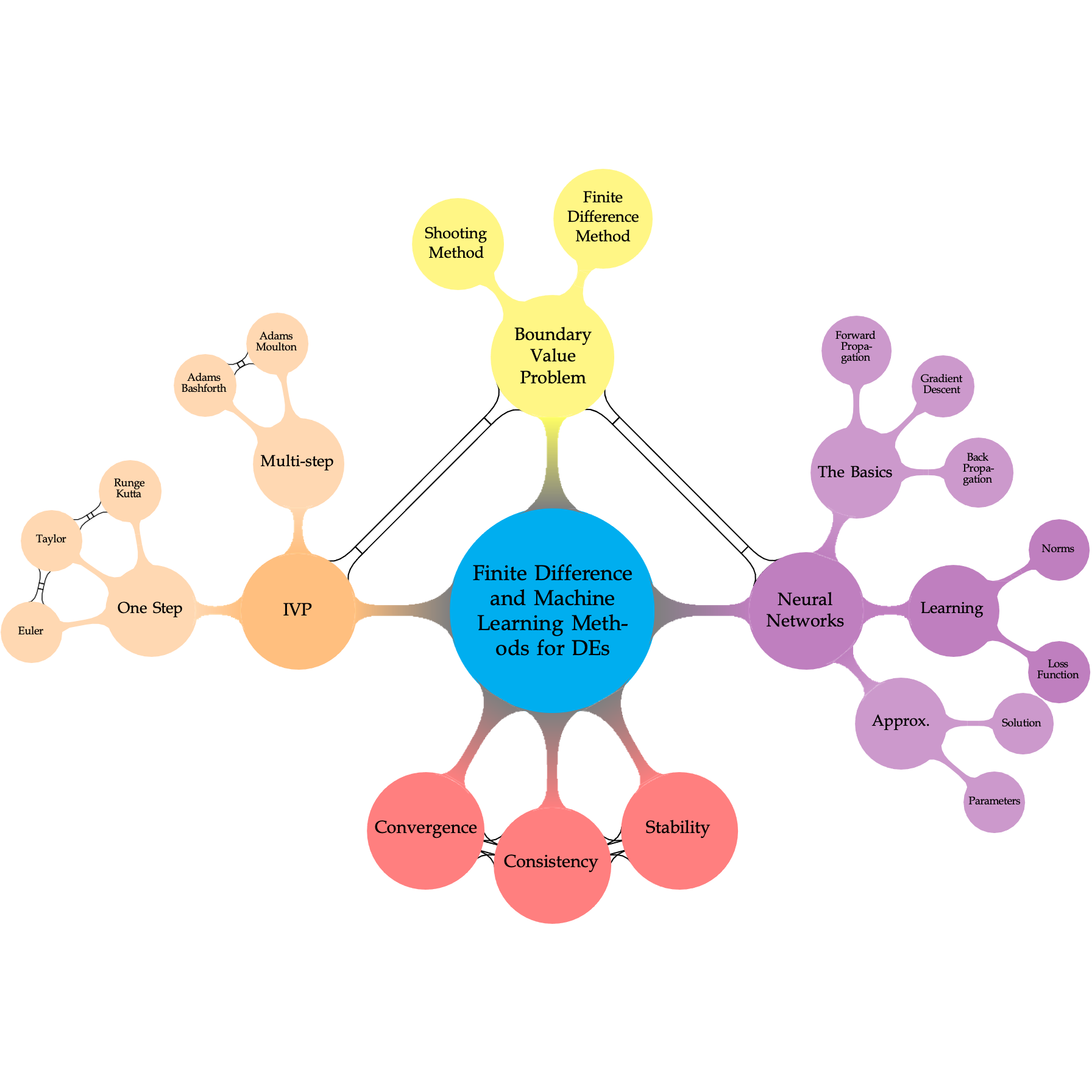
Back Progagation ReLU three inputs#

Gradient descent to train a simple artificial neural network (ANN) with one input node, one hidden node (using the ReLU activation function), and one output node. We will use a basic regression problem as an example.

Problem Statement: We want to train a neural network to predict the output (y) based on a single input feature (x). The network architecture is as follows:

  1. Input layer: One neuron with input \(x\).

  2. Hidden layer: One neuron with weight \(w\) and bias \(b\), applying the ReLU activation function.

  3. Output layer: One neuron with weight \(v\) and bias \(c\), representing the predicted output.

The network’s output \(y\) can be expressed as:

\[y = v \cdot \text{ReLU}(w \cdot x + b) + c\]

Data: Let’s assume we have a dataset with input-output pairs (x, y) for training:

\[\begin{split} \begin{align*} (x_1, y_1) &= (2.0, 2.0) \\ (x_2, y_2) &= (3.0, 3.0) \\ (x_3, y_3) &= (4.0, 4.0) \\ \end{align*} \end{split}\]

Initialization:

  • Initialize the parameters randomly or with predetermined values:

    • \(w = 0.5\)

    • \(b = 0.2\)

    • \(v = 0.3\)

    • \(c = 0.1\)

  • Set the learning rate \(\alpha\) (e.g., \(\alpha = 0.1\)).

Training: We’ll use gradient descent to update the network parameters in order to minimize the mean squared error (MSE) cost function:

\[J(\theta) = \frac{1}{2N} \sum_{i=1}^N (y_i - y_{\text{target},i})^2\]

where \(N\) is the number of training examples, \(y_i\) is the predicted output for the \(i\)-th example, and \(y_{\text{target},i}\) is the target output for the \(i\)-th example.

Here’s how we update the parameters in each training iteration:

  1. For each training example (x, y), calculate the predicted output \(y\) using the current network parameters:

    \[y = v \cdot \text{ReLU}(w \cdot x + b) + c\]

  2. Calculate the cost for this example:

    \[J(\theta) = \frac{1}{2}(y - y_{\text{target}})^2\]

  3. Compute the gradients of the cost with respect to the parameters:

    • \(\frac{\partial J}{\partial v} = y - y_{\text{target}}\)

    • \(\frac{\partial J}{\partial c} = y - y_{\text{target}}\)

    • \(\frac{\partial J}{\partial w} = \frac{\partial J}{\partial y} \cdot \frac{\partial y}{\partial \text{ReLU}} \cdot \frac{\partial \text{ReLU}}{\partial(w \cdot x + b)} \cdot \frac{\partial(w \cdot x + b)}{\partial w}\)

    • \(\frac{\partial J}{\partial b} = \frac{\partial J}{\partial y} \cdot \frac{\partial y}{\partial \text{ReLU}} \cdot \frac{\partial \text{ReLU}}{\partial(w \cdot x + b)} \cdot \frac{\partial(w \cdot x + b)}{\partial b}\)

  4. Update the parameters using gradient descent:

    • \(v = v - \alpha \cdot \frac{\partial J}{\partial v}\)

    • \(c = c - \alpha \cdot \frac{\partial J}{\partial c}\)

    • \(w = w - \alpha \cdot \frac{\partial J}{\partial w}\)

    • \(b = b - \alpha \cdot \frac{\partial J}{\partial b}\)

Repeat steps 1-4 for a specified number of training iterations or until the cost converges to a minimum. In each iteration, you use the gradients to adjust the parameters in the direction that minimizes the cost function, thus training the neural network.

This example illustrates a basic gradient descent approach for training a simple neural network with ReLU activation. In practice, real-world scenarios involve larger networks, more data, and libraries like TensorFlow or PyTorch to handle the training process efficiently.

import numpy as np

# Define the neural network architecture
def relu(x):
    return np.maximum(0, x)

# Initialize the network parameters
w = 0.5
b = 0.2
v = 0.3
c = 0.1
learning_rate = 0.1

# Define the training data
x = 2.0
y_target = 2.0

# Forward pass
z = w * x + b
h = relu(z)
y = v * h + c

# Compute the cost
cost = 0.5 * (y - y_target)**2

# Compute the gradients
dJ_dy = y - y_target
dJ_dv = dJ_dy * h
dJ_dc = dJ_dy
dJ_dh = dJ_dy * v
dJ_dz = dJ_dh if z > 0 else 0
dJ_dw = dJ_dz * x
dJ_db = dJ_dz

# Update the parameters using gradient descent
v -= learning_rate * dJ_dv
c -= learning_rate * dJ_dc
w -= learning_rate * dJ_dw
b -= learning_rate * dJ_db

# Print the updated parameters
print(f"Updated w: {w}")
print(f"Updated b: {b}")
print(f"Updated v: {v}")
print(f"Updated c: {c}")

Updated w: 0.5924
Updated b: 0.2462
Updated v: 0.4848
Updated c: 0.254