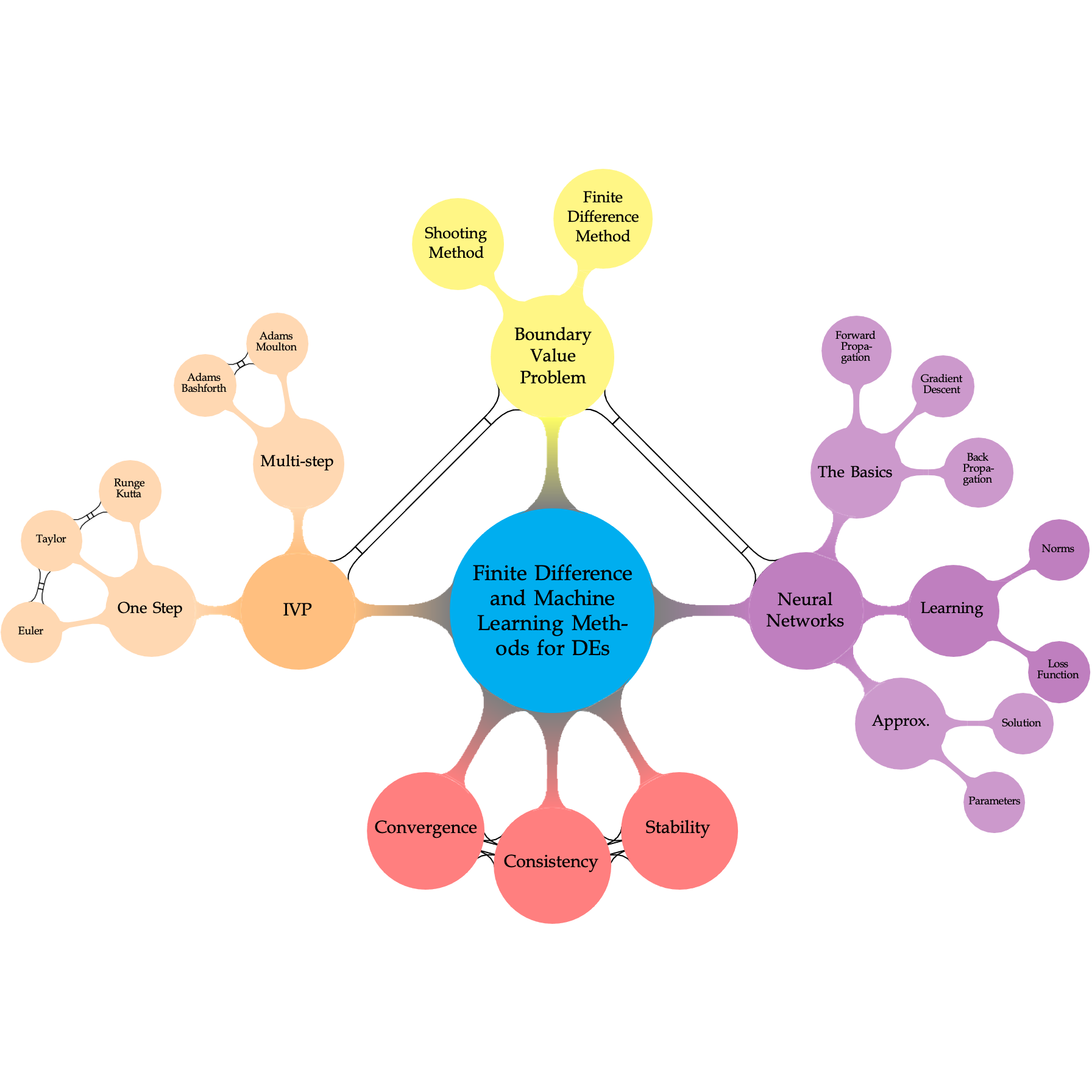
The Perceptron

The perceptron is a fundamental concept in the field of artificial neural networks and machine learning. It was introduced by Frank Rosenblatt in the late 1950s and is a simplified model of a biological neuron. Here’s a summary of the perceptron:

Structure: The perceptron is a simple neural network model with the following components:

1. Input Features: It takes a set of input features \((x_1, x_2, \ldots, x_n\)).

2. Weights: Each input feature is associated with a weight \((w_1, w_2, \ldots, w_n\)), which represents the strength of the connection from the input to the perceptron.

3. Summation Function: It calculates the weighted sum of the input features and weights:

\[ z = w_1x_1 + w_2x_2 + \ldots + w_nx_n\]

4. Activation Function: The perceptron uses a threshold activation function (typically a step function) to make a binary decision based on the weighted sum.

Operation: The perceptron operates as follows:

1. It receives input features \(x_1, x_2, \ldots, x_n\) along with associated weights \(w_1, w_2, \ldots, w_n\).

2. It calculates the weighted sum \(z = w_1x_1 + w_2x_2 + \ldots + w_nx_n\).

3. It applies the threshold activation function, comparing the weighted sum \(z\) to a predefined threshold value.

4. If \(z\) is greater than or equal to the threshold, the perceptron outputs 1 (or “fires”). If \(z\) is less than the threshold, it outputs 0 (or remains inactive).

Learning: The perceptron can be trained to adjust its weights by using a simple learning rule, such as the perceptron learning rule, which updates the weights based on the error in the output.

Limitations: The perceptron is a linear binary classifier and has several limitations:

• It can only represent linear decision boundaries.

• It cannot solve problems that are not linearly separable.

• It does not perform well on more complex tasks.

import numpy as np

class Perceptron:
    def __init__(self, input_size, learning_rate=0.1, epochs=100):
        self.weights = np.random.rand(input_size)
        self.bias = 0
        self.learning_rate = learning_rate
        self.epochs = epochs

    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    def predict(self, inputs):
        weighted_sum = np.dot(inputs, self.weights) + self.bias
        return self.sigmoid(weighted_sum)

    def train(self, training_data, labels):
        for epoch in range(self.epochs):
            for i in range(len(training_data)):
                inputs = training_data[i]
                prediction = self.predict(inputs)
                label = labels[i]

                # Update weights and bias
                error = label - prediction
                self.weights += self.learning_rate * error * prediction * (1 - prediction) * inputs
                self.bias += self.learning_rate * error

    def evaluate(self, test_data, labels):
        correct = 0
        total = len(test_data)

        for i in range(total):
            inputs = test_data[i]
            prediction = round(self.predict(inputs))
            label = labels[i]

            if prediction == label:
                correct += 1

        accuracy = (correct / total) * 100
        return accuracy

# Example usage
if __name__ == '__main__':
    # Define training data and labels
    training_data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
    labels = np.array([0, 0, 0, 1])

    # Create a Perceptron
    perceptron = Perceptron(input_size=2, learning_rate=0.1, epochs=1000)

    # Train the Perceptron
    perceptron.train(training_data, labels)

    # Define test data
    test_data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])

    # Evaluate the Perceptron
    accuracy = perceptron.evaluate(test_data, labels)
    print(f"Accuracy: {accuracy:.2f}%")

Accuracy: 100.00%