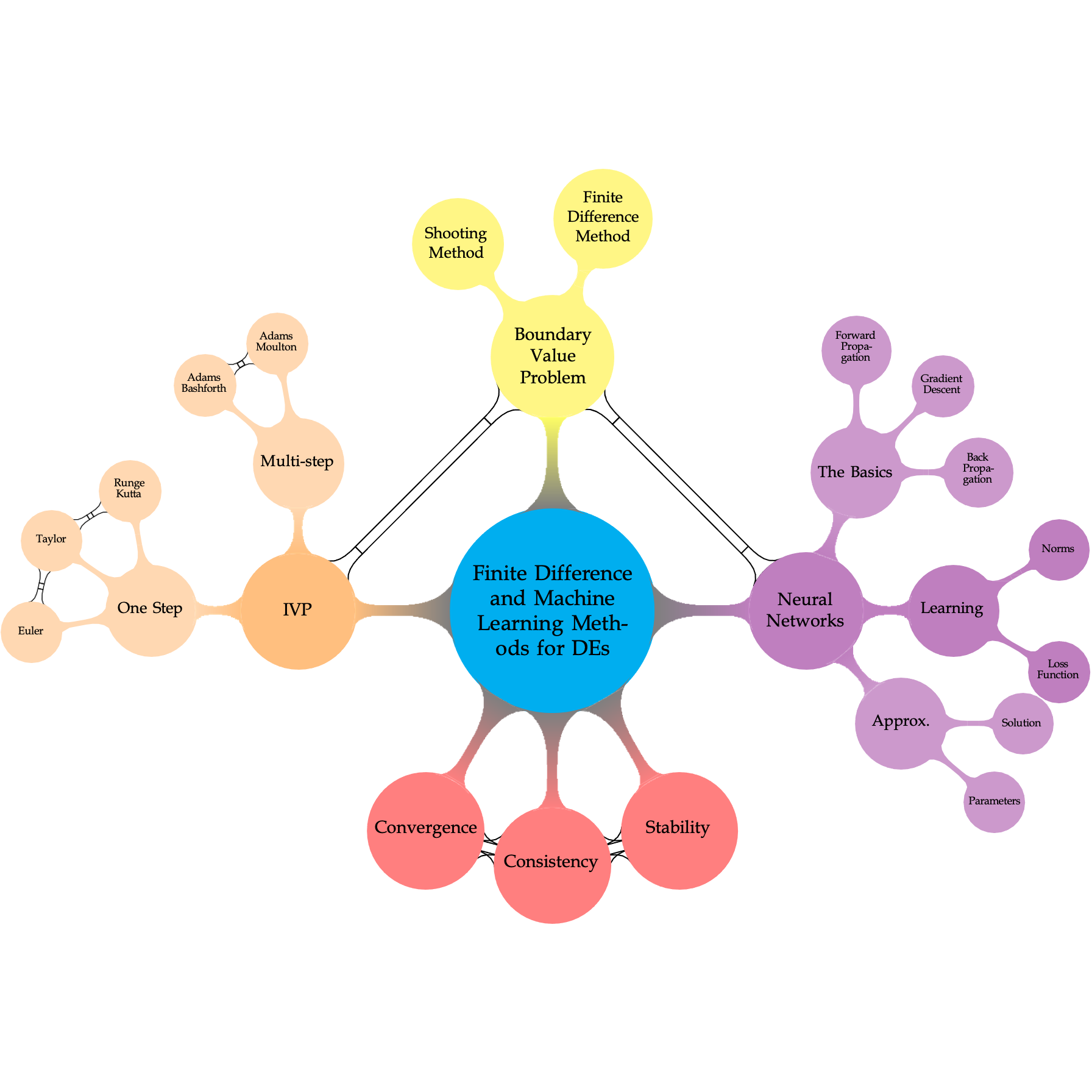
Three Layer Feed Forward ANN#

The mathematical calculations for a simple artificial neural network (ANN) with two hidden layers, each having three ReLU (Rectified Linear Unit) nodes, and an output layer with a Sigmoid activation function. Let’s denote the inputs as \(x_1\), \(x_2\), and \(x_3\), the weights for the connections between the input layer and the first hidden layer as \(w_{ij}^{(1)}\) (where \(i\) represents the input node, and \(j\) represents the hidden node), the biases for the first hidden layer as \(b_j^{(1)}\), the weights for the connections between the first hidden layer and the second hidden layer as \(w_{jk}^{(2)}\), the biases for the second hidden layer as \(b_k^{(2)}\), the weights for the connections between the second hidden layer and the output layer as \(w_{kl}^{(3)}\), and the bias for the output layer as \(b_l^{(3)}\).

The calculations for the nodes in the first hidden layer (\(h_1^{(1)}\), \(h_2^{(1)}\), and \(h_3^{(1)}\)) are as follows:

\[ h_1^{(1)} = \text{ReLU}(w_{11}^{(1)}x_1 + w_{21}^{(1)}x_2 + w_{31}^{(1)}x_3 + b_1^{(1)}) \]
\[ h_2^{(1)} = \text{ReLU}(w_{12}^{(1)}x_1 + w_{22}^{(1)}x_2 + w_{32}^{(1)}x_3 + b_2^{(1)}) \]
\[ h_3^{(1)} = \text{ReLU}(w_{13}^{(1)}x_1 + w_{23}^{(1)}x_2 + w_{33}^{(1)}x_3 + b_3^{(1)}) \]

The ReLU function is defined as \(\text{ReLU}(x) = \max(0, x)\), meaning that it outputs the input value if it is positive and zero otherwise.

The calculations for the nodes in the second hidden layer (\(h_1^{(2)}\), \(h_2^{(2)}\), and \(h_3^{(2)}\)) are similar:

\[ h_1^{(2)} = \text{ReLU}(w_{11}^{(2)}h_1^{(1)} + w_{21}^{(2)}h_2^{(1)} + w_{31}^{(2)}h_3^{(1)} + b_1^{(2)}) \]
\[ h_2^{(2)} = \text{ReLU}(w_{12}^{(2)}h_1^{(1)} + w_{22}^{(2)}h_2^{(1)} + w_{32}^{(2)}h_3^{(1)} + b_2^{(2)}) \]
\[ h_3^{(2)} = \text{ReLU}(w_{13}^{(2)}h_1^{(1)} + w_{23}^{(2)}h_2^{(1)} + w_{33}^{(2)}h_3^{(1)} + b_3^{(2)}) \]

Finally, the calculation for the output node (\(y\)) with the Sigmoid activation function is:

\[ y = \text{Sigmoid}(w_{11}^{(3)}h_1^{(2)} + w_{21}^{(3)}h_2^{(2)} + w_{31}^{(3)}h_3^{(2)} + b^{(3)}) \]

Where \(\text{Sigmoid}(x) = \frac{1}{1 + e^{-x}}\) is the sigmoid function that squashes the output value between 0 and 1.

import numpy as np

# Define the neural network architecture
input_size = 3  # Number of input features
hidden_size1 = 3  # Number of nodes in the hidden layer
hidden_size2 = 3  # Number of nodes in the hidden layer
output_size = 1  # Number of output nodes

# Initialize random weights and biases
np.random.seed(0)
input_layer_size = input_size
hidden_layer1_size = hidden_size1
hidden_layer2_size = hidden_size2
output_layer_size = output_size

# Initialize weights and biases with random values
weights_input_hidden1 = np.random.randn(input_layer_size, hidden_layer1_size)
bias_hidden1 = np.zeros((1, hidden_layer1_size))
# Initialize weights and biases with random values
weights_input_hidden2 = np.random.randn(hidden_layer1_size, hidden_layer2_size)
bias_hidden2 = np.zeros((1, hidden_layer2_size))
weights_hidden_output = np.random.randn(hidden_layer2_size, output_layer_size)
bias_output = np.zeros((1, output_size))

# Define the sigmoid activation function
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# Define the ReLU activation function
def ReLU(x):
    return np.maximum(0,x)


# Define the forward propagation function
def forward_propagation(X):
    # Calculate the values for the hidden layer 1
    hidden_input1 = np.dot(X.T, weights_input_hidden1) + bias_hidden1
    hidden_output1 = ReLU(hidden_input1)

    # Calculate the values for the hidden layer 2
    hidden_input2 = np.dot(hidden_output1, weights_input_hidden2) + bias_hidden2
    hidden_output2 = ReLU(hidden_input2)

    # Calculate the values for the output layer
    output_input = np.dot(hidden_output2, weights_hidden_output) + bias_output
    output = sigmoid(output_input)
    
    return hidden_input1, hidden_output1,hidden_input2, hidden_output2, output_input, output

# Example input data
X = np.array([[0, 0, 1], [0, 1, 0]]).T  # Two input samples

# Perform forward propagation
hidden_input1, hidden_output1,hidden_input2, hidden_output2,  output_input, output = forward_propagation(X)

# Print the output
print("Output:")
print(output)

Output:
[[2.86873055e-02]
 [3.81899579e-05]]

Outline of the Maths for an ANN#

  1. Input Layer:

    • Input data: X

  2. First Hidden Layer:

    • Number of nodes: 3

    • Weight matrix: W1 (3x3)

    • Bias vector: b1 (1x3)

    • Activation function: ReLU (Rectified Linear Unit)

The output of the first hidden layer (Z1) is calculated as follows:

Z1 = X * W1 + b1

Where:

  • X is the input data (a row vector),

  • W1 is the weight matrix for the first hidden layer,

  • b1 is the bias vector for the first hidden layer,

  • “*” represents matrix multiplication.

  1. Apply ReLU activation to Z1:

    A1 = ReLU(Z1)

    A1 is the output of the first hidden layer.

  2. Second Hidden Layer:

    • Number of nodes: 3

    • Weight matrix: W2 (3x3)

    • Bias vector: b2 (1x3)

    • Activation function: ReLU

The output of the second hidden layer (Z2) is calculated in the same way as the first hidden layer:

Z2 = A1 * W2 + b2

  1. Apply ReLU activation to Z2:

    A2 = ReLU(Z2)

    A2 is the output of the second hidden layer.

  2. Output Layer:

    • Number of nodes: 1

    • Weight matrix: W3 (3x1)

    • Bias vector: b3 (1x1)

    • Activation function: Sigmoid

The output of the output layer (Z3) is calculated as:

Z3 = A2 * W3 + b3

  1. Apply the Sigmoid activation to Z3 to get the final output (Y):

    Y = Sigmoid(Z3)

This is the forward pass of the network, and it calculates the output based on the given input data.