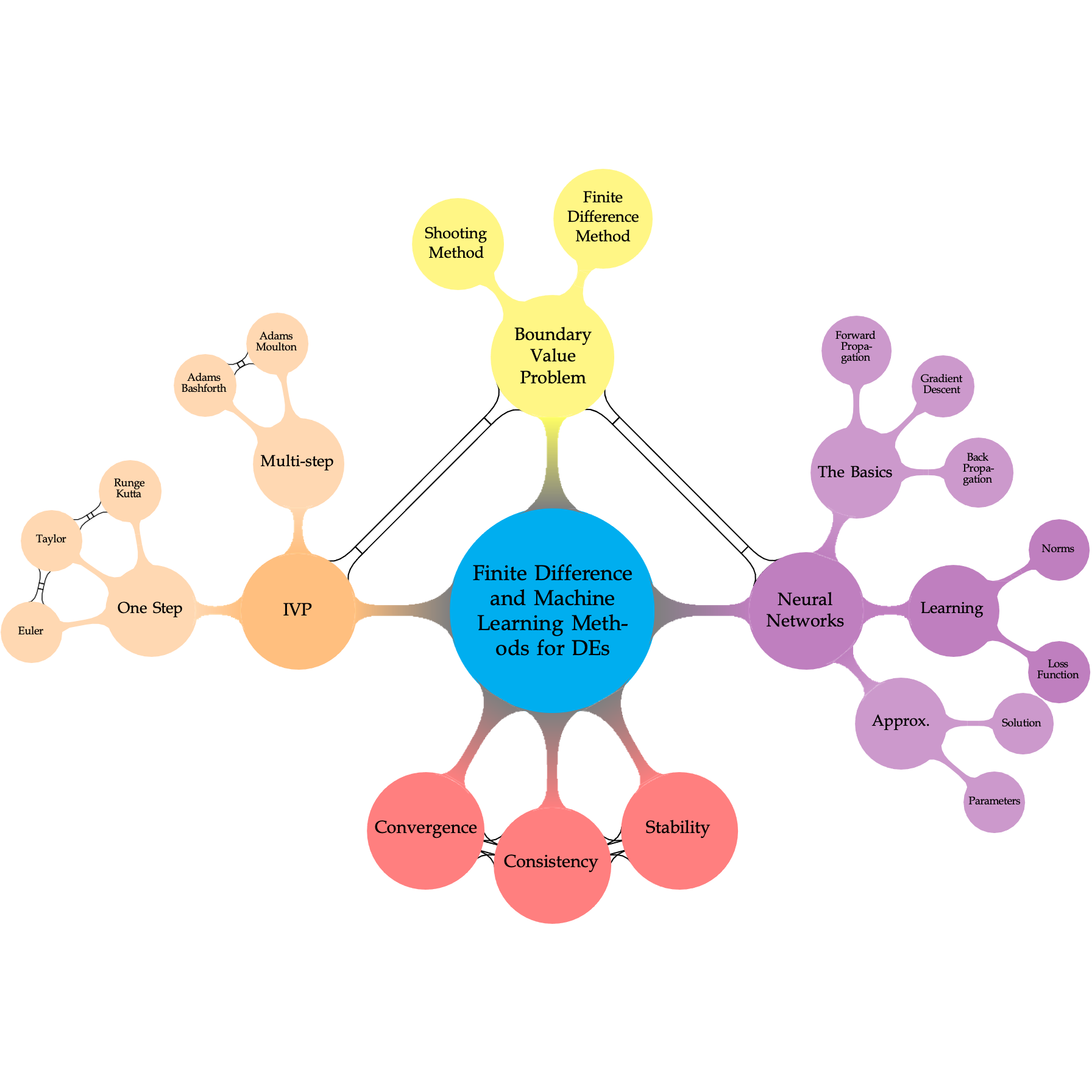
Problem Sheet 5 - Consistency, Convergence and Stability

Question 1

1. Determine whether the 2-step Adams-Bashforth Method is consistent, convergent and stable

(408)$$w_{n+1}=w_n+(\frac{3}{2}hf(t_n,w_n)-\frac{1}{2}hf(t_{n-1},w_{n-1})).$$

Question 2

2. Determine whether the 2-step Adams-Moulton Method is consistent, convergent and stable

(409)$$w_{n+1}=w_n+\frac{5}{12}hf(t_{n+1},w_{n+1})+\frac{8}{12}hf(t_n,w_n)-\frac{1}{12}hf(t_{n-1},w_{n-1}).$$

Question 3

3. Determine whether the linear multistep following methods are consistent, convergent and stable:

(410)$$w_{n+1}=w_{n-1}+\frac{1}{3}h[f(t_{n+1},w_{n+1})+4f(t_n,w_n)+f(t_{n-1},w_{n-1})].$$

(411)$$w_{n+1}=\frac{4}{3}{w}_n-\frac{1}{3}{w}_{n-1}+\frac{2}{3}h[f(t_{n+1},w_{n+1})].$$

Question 4

4. In your own words discuss the following concepts and their relevance for the one-step methods for approximating the solution to initial value problems:

a. consistency of the numerical methods;

b. convergence of the numerical methods;

c. stability of the numerical methods.

Illustrate your answers by stating conditions which are required.

Question 5

5. In your own words discuss the following concepts and their relevance for the Adams-Bashforth and Adams-Moulton methods for approximating the solution to initial value problems:

a. implicit and explicit numerical methods;

b. consistency of the numerical methods;

c. convergence of the numerical methods;

d. stability of the numerical methods.

Illustrate your answers by stating conditions which are required.