Problem Sheet 2 Question 5 - 2nd Order Taylor

The general form of the population growth differential equation

(276)\[\begin{equation} y^{'}=f(t,y), \ \ (a \leq t \leq b)\end{equation}\]

with the initial condition

(277)\[\begin{equation} y(a)=A .\end{equation}\]

Apply 2nd Order Taylor to approximate the solution of the given initial value problems using the indicated number of time steps. Compare the approximate solution with the given exact solution, and compare the actual error with the theoretical error.

## Library
import numpy as np
import math 

%matplotlib inline
import matplotlib.pyplot as plt # side-stepping mpl backend
import matplotlib.gridspec as gridspec # subplots
import warnings
import pandas as pd

warnings.filterwarnings("ignore")

General Discrete Interval

The continuous time \(a\leq t \leq b \) is discretised into \(N\) points seperated by a constant stepsize

(278)\[\begin{equation} h=\frac{b-a}{N}.\end{equation}\]

Specific Discrete Interval

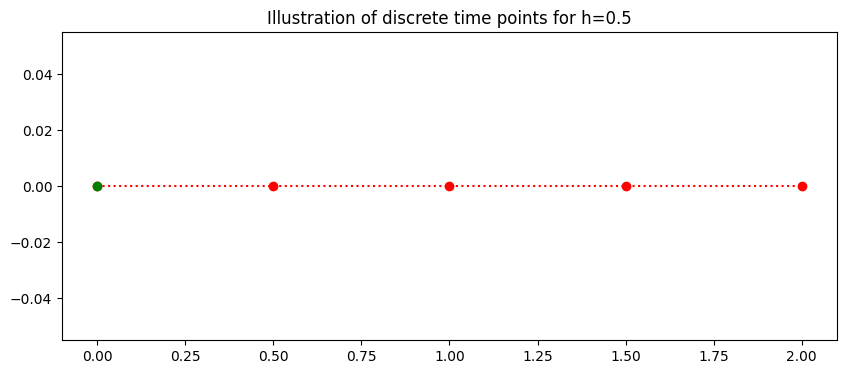
Here the interval is \(0\leq t \leq 2\) with \(N=4\)

(279)\[\begin{equation} h=\frac{2-0}{4}=0.5.\end{equation}\]

This gives the 5 discrete points with stepsize h=0.5:

(280)\[\begin{equation} t_0=0, \ t_1=0.5, \ ... t_{4}=2. \end{equation}\]

This is generalised to

(281)\[\begin{equation} t_i=0+i0.5, \ \ \ i=0,1,...,4.\end{equation}\]

The plot below illustrates the discrete time steps from 0 to 2.

### Setting up time
t_end=2
t_start=0
N=4
h=(t_end-t_start)/(N)
t=np.arange(t_start,t_end+0.01,h)
fig = plt.figure(figsize=(10,4))
plt.plot(t,0*t,'o:',color='red')
plt.plot(t[0],0*t[0],'o',color='green')


plt.title('Illustration of discrete time points for h=%s'%(h))
plt.plot();

2nd Order Taylor Solution

The 2nd Order Taylor difference equation is given by

(282)\[\begin{equation} w_{i+1}=w_i+h\left[f(t_i,w_i)+\frac{h}{2}f'(t_i,w_i)\right],\end{equation}\]

where

(283)\[\begin{equation} f(t_i,w_i)=????,\end{equation}\]

and

(284)\[\begin{equation} f'(t_i,w_i)=???,\end{equation}\]

which gives

(285)\[\begin{equation} w_{i+1}=w_i+h????,\end{equation}\]

for \(i=0,1,2,N-1\) with \(w_0=A\)

IC=0.5
w=np.zeros(N+1)
e=np.zeros(N+1)
w[0]=IC

for i in range (0,N):
    ###
##    w[i+1]=w[i]+h*(????)

  File "/var/folders/1r/rb8x65yn57q68x042jv2vgx80000gn/T/ipykernel_81530/1336265521.py", line 8
    ##    w[i+1]=w[i]+h*(????)
                              ^
SyntaxError: unexpected EOF while parsing

fig = plt.figure(figsize=(4,5))
# --- left hand plot
#ax = fig.add_subplot(1,4,1)
plt.plot(t,w,'o:',color='k')
plt.plot(t[0],w[0],'o',color='green')


#ax.legend(loc='best')
plt.title('Numerical Solution (w) h=%s'%(h))
plt.show()

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
/var/folders/1r/rb8x65yn57q68x042jv2vgx80000gn/T/ipykernel_81530/3144700355.py in <module>
      2 # --- left hand plot
      3 #ax = fig.add_subplot(1,4,1)
----> 4 plt.plot(t,w,'o:',color='k')
      5 plt.plot(t[0],w[0],'o',color='green')
      6 

NameError: name 'w' is not defined

<Figure size 400x500 with 0 Axes>

d = {'time t_i': t,      'Taylor (w_i) ':w}
df = pd.DataFrame(data=d)
df

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
/var/folders/1r/rb8x65yn57q68x042jv2vgx80000gn/T/ipykernel_81530/3734270711.py in <module>
----> 1 d = {'time t_i': t,      'Taylor (w_i) ':w}
      2 df = pd.DataFrame(data=d)
      3 df

NameError: name 'w' is not defined