Finite Difference Methods for the Poisson Equation¶

This notebook will focus on numerically approximating a inhomogenous second order Poisson Equation.

The Differential Equation¶

The general two dimensional Poisson Equation is of the form: $$ \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial x^2}=f(x,y), \ \ \ (x,y) \in \Omega=(0,1)\times (0,1),$$ with boundary conditions $$U(x,y) = g(x,y), \ \ \ (x,y)\in\delta\Omega\text{ - boundary}. $$

Homogenous Poisson Equation¶

This notebook will implement a finite difference scheme to approximate the inhomogenous form of the Poisson Equation $f(x,y)=100(x^2+y^2)$: $$ \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial x^2}=100(x^2+y^2).$$ with the Boundary Conditions: $$ u(x,0)=\sin(2\pi x), \ \ \ \ \ 0 \leq x \leq 1, \text{ lower},$$ u(x,1)=\sin(2\pi x), \ \ \ \ \ 0 \leq x \leq 1, \text{ upper},$$ u(0,y)=2\sin(2\pi y), \ \ \ \ \ 0 \leq y \leq 1, \text{ left},$$ u(1,y)=2\sin(2\pi y), \ \ \ \ \ 0 \leq y \leq 1, \text{ right}.$$

# LIBRARY
# vector manipulation
import numpy as np
# math functions
import math 

# THIS IS FOR PLOTTING
%matplotlib inline
import matplotlib.pyplot as plt # side-stepping mpl backend
import warnings
warnings.filterwarnings("ignore")
from IPython.display import HTML
from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt

Discete Grid¶

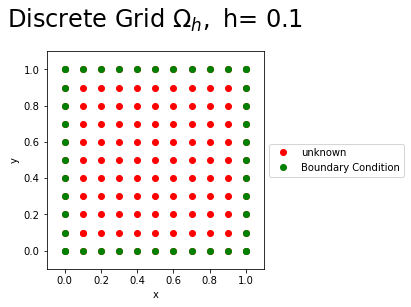
The region $\Omega=(0,1)\times(0,1)$ is discretised into a uniform mesh $\Omega_h$. In the $x$ and $y$ directions into $N$ steps giving a stepsize of $$ h=\frac{1-0}{N},$$ resulting in $$x[i]=0+ih, \ \ \ i=0,1,...,N,$$ and $$x[j]=0+jh, \ \ \ j=0,1,...,N,$$ The Figure below shows the discrete grid points for $N=10$, the known boundary conditions (green), and the unknown values (red) of the Poisson Equation.

N=10
h=1/N
x=np.arange(0,1.0001,h)
y=np.arange(0,1.0001,h)
X, Y = np.meshgrid(x, y)
fig = plt.figure()
plt.plot(x[1],y[1],'ro',label='unknown');
plt.plot(X,Y,'ro');
plt.plot(np.ones(N+1),y,'go',label='Boundary Condition');
plt.plot(np.zeros(N+1),y,'go');
plt.plot(x,np.zeros(N+1),'go');
plt.plot(x, np.ones(N+1),'go');
plt.xlim((-0.1,1.1))
plt.ylim((-0.1,1.1))
plt.xlabel('x')
plt.ylabel('y')
plt.gca().set_aspect('equal', adjustable='box')
plt.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.title(r'Discrete Grid $\Omega_h,$ h= %s'%(h),fontsize=24,y=1.08)
plt.show();

../_images/903_Poisson_Equation_Boundary_3_0.png

Boundary Conditions¶

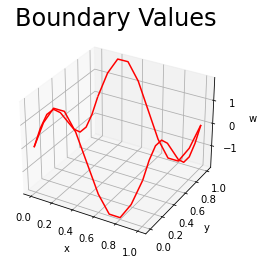
The discrete boundary conditions are $$ w_{i0}=w[i,0]=\sin(2\pi x[i]), \text{ for } i=0,...,10, \text{ upper},$$

\[ w_{iN}=w[i,N]=\sin(2\pi x[i]), \text{ for } i=0,...,10, \text{ lower},\]

\[ w_{0j}=w[0,j]=2\sin(2\pi y[j]), \text{ for } j=0,...,10, \text{ left},\]

\[ w_{Nj}=w[N,j]=2\sin(2\pi y[j]), \text{ for } i=0,...,10,\text{ right}. \]

The Figure below plots the boundary values of $w[i,j]$.

w=np.zeros((N+1,N+1))

for i in range (0,N):
        w[i,0]=np.sin(2*np.pi*x[i]) #left Boundary
        w[i,N]=np.sin(2*np.pi*x[i]) #Right Boundary

for j in range (0,N):
        w[0,j]=2*np.sin(2*np.pi*y[j]) #Lower Boundary
        w[N,j]=2*np.sin(2*np.pi*y[j]) #Upper Boundary

        
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Plot a basic wireframe.
ax.plot_wireframe(X, Y, w,color='r', rstride=10, cstride=10)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('w')
plt.title(r'Boundary Values',fontsize=24,y=1.08)
plt.show()

../_images/903_Poisson_Equation_Boundary_5_0.png

Numerical Method¶

The Poisson Equation is discretised using $\delta_x^2$ is the central difference approximation of the second derivative in the $x$ direction $$\delta_x^2=\frac{1}{h^2}(w_{i+1j}-2w_{ij}+w_{i-1j}), $$ and $\delta_y^2$ is the central difference approximation of the second derivative in the $y$ direction $$\delta_y^2=\frac{1}{h^2}(w_{ij+1}-2w_{ij}+w_{ij-1}). $$ The gives the Poisson Difference Equation, $$-(\delta_x^2w_{ij}+\delta_y^2w_{ij})=f_{ij} \ \ (x_i,y_j) \in \Omega_h, $$w_{ij}=g_{ij} \ \ (x_i,y_j) \in \partial\Omega_h, $$ where $w_ij$ is the numerical approximation of $U$ at $x_i$ and $y_j$. Expanding the the Poisson Difference Equation gives the five point method, $$-(w_{i-1j}+w_{ij-1}-4w_{ij}+w_{ij+1}+w_{i+1j})=h^2f_{ij} $$ for $i=1,…,N-1$ and $j=1,…,N-1.$

Matrix form¶

This can be written as a system of $(N-1)\times(N-1)$ equations can be arranged in matrix form $$ A\mathbf{w}=\mathbf{r},$$ where $A$ is an $(N-1)^2\times(N-1)^2$ matrix made up of the following block tridiagonal structure $$\left(\begin{array}{ccccccc} T&I&0&0&.&.&.\\ I&T&I&0&0&.&.\\ .&.&.&.&.&.&.\\ .&.&.&0&I&T&I\\ .&.&.&.&0&I&T\\ \end{array}\right), $$ where $I$ denotes an $N-1 \times N-1$ identity matrix and $T$ is the tridiagonal matrix of the form: $$ T=\left(\begin{array}{ccccccc} -4&1&0&0&.&.&.\\ 1&-4&1&0&0&.&.\\ .&.&.&.&.&.&.\\ .&.&.&0&1&-4&1\\ .&.&.&.&0&1&-4\\ \end{array}\right). $$ The plot below shows the matrix $A$ and its inverse $A^{-1}$ as a colourplot.

N2=(N-1)*(N-1)
A=np.zeros((N2,N2))
## Diagonal            
for i in range (0,N-1):
    for j in range (0,N-1):           
        A[i+(N-1)*j,i+(N-1)*j]=-4

# LOWER DIAGONAL        
for i in range (1,N-1):
    for j in range (0,N-1):           
        A[i+(N-1)*j,i+(N-1)*j-1]=1   
# UPPPER DIAGONAL        
for i in range (0,N-2):
    for j in range (0,N-1):           
        A[i+(N-1)*j,i+(N-1)*j+1]=1   

# LOWER IDENTITY MATRIX
for i in range (0,N-1):
    for j in range (1,N-1):           
        A[i+(N-1)*j,i+(N-1)*(j-1)]=1        
        
        
# UPPER IDENTITY MATRIX
for i in range (0,N-1):
    for j in range (0,N-2):           
        A[i+(N-1)*j,i+(N-1)*(j+1)]=1
Ainv=np.linalg.inv(A)   
fig = plt.figure(figsize=(12,4));
plt.subplot(121)
plt.imshow(A,interpolation='none');
clb=plt.colorbar();
clb.set_label('Matrix elements values');
plt.title('Matrix A ',fontsize=24)
plt.subplot(122)
plt.imshow(Ainv,interpolation='none');
clb=plt.colorbar();
clb.set_label('Matrix elements values');
plt.title(r'Matrix $A^{-1}$ ',fontsize=24)

fig.tight_layout()
plt.show();

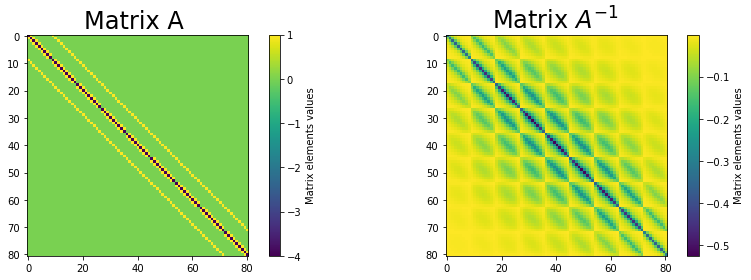
../_images/903_Poisson_Equation_Boundary_7_0.png

The vector $\mathbf{w}$ is of length $(N-1)\times(N-1)$ which made up of $N-1$ subvectors $\mathbf{w}_j$ of length $N-1$ of the form $$\mathbf{w}_j=\left(\begin{array}{c} w_{1j}\\ w_{2j}\\ .\\ .\\ w_{N-2j}\\ w_{N-1j}\\ \end{array}\right). $$ The vector $\mathbf{r}$ is of length $(N-1)\times(N-1)$ which made up of $N-1$ subvectors of the form $\mathbf{r}_j=-h^2\mathbf{f}j-\mathbf{bx}{j}-\mathbf{by}_j$, where $\mathbf{bx}_j $ is the vector of left and right boundary conditions $$\mathbf{bx}_j =\left(\begin{array}{c} w_{0j}\\ 0\\ .\\ .\\ 0\\ w_{Nj} \end{array}\right), $$

for $j=1,..,N-1$, where $\mathbf{by}_j$ is the vector of the lower boundary condition for $j=1$,

\[\begin{split} \mathbf{by}_{1} =\left(\begin{array}{c} w_{10}\\ w_{20}\\ .\\ .\\ w_{N-20}\\ w_{N-10}\\ \end{array}\right), \end{split}\]

upper boundary condition for $j=N-1$

\[\begin{split} \mathbf{by}_{N-1} =\left(\begin{array}{c} w_{1N}\\ w_{2N}\\ .\\ .\\ w_{N-2N}\\ w_{N-1N}\\ \end{array}\right), \end{split}\]

for $j=2,...,N-2$ $$\mathbf{by}_j=0,$$ and $$\mathbf{f}_j =100\left(\begin{array}{c} x_1^2+y_j^2\\ x_2^2+y_j^2\\ .\\ .\\ x_{N-2}^2+y_j^2\\ x_{N-1}^2+y_j^2 \end{array}\right) $$ for $j=1,…,N-1$.

r=np.zeros(N2)

# vector r      
for i in range (0,N-1):
    for j in range (0,N-1):           
        r[i+(N-1)*j]=100*h*h*(x[i+1]*x[i+1]+y[j+1]*y[j+1])     
# Boundary        
b_bottom_top=np.zeros(N2)
for i in range (0,N-1):
    b_bottom_top[i]=np.sin(2*np.pi*x[i+1]) #Bottom Boundary
    b_bottom_top[i+(N-1)*(N-2)]=np.sin(2*np.pi*x[i+1])# Top Boundary
      
b_left_right=np.zeros(N2)
for j in range (0,N-1):
    b_left_right[(N-1)*j]=2*np.sin(2*np.pi*y[j+1]) # Left Boundary
    b_left_right[N-2+(N-1)*j]=2*np.sin(2*np.pi*y[j+1])# Right Boundary
    
b=b_left_right+b_bottom_top

Results¶

To solve the system for $\mathbf{w}$ invert the matrix $A$ $$ A\mathbf{w}=\mathbf{r},$$ such that $$ \mathbf{w}=A^{-1}\mathbf{r}.$$ Lastly, as $\mathbf{w}$ is in vector it has to be reshaped into grid form to plot.

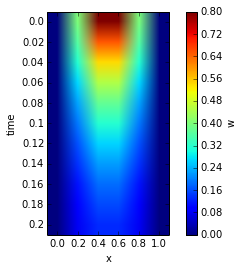
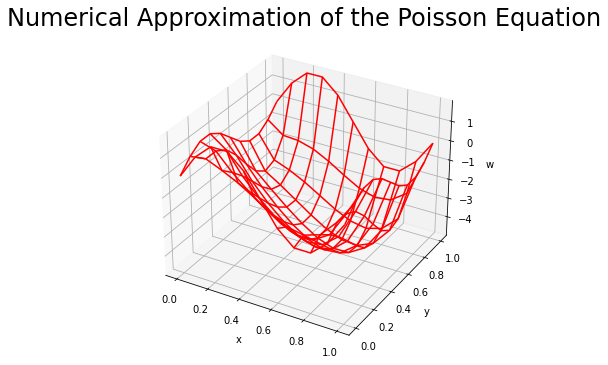
The figure below shows the numerical approximation of the homogeneous Equation.

C=np.dot(Ainv,r-b)
w[1:N,1:N]=C.reshape((N-1,N-1))

fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d');
# Plot a basic wireframe.
ax.plot_wireframe(X, Y, w,color='r');
ax.set_xlabel('x');
ax.set_ylabel('y');
ax.set_zlabel('w');
plt.title(r'Numerical Approximation of the Poisson Equation',fontsize=24,y=1.08);
plt.show();

../_images/903_Poisson_Equation_Boundary_11_0.png

Numerical Analysis

Finite Difference Methods for the Poisson Equation¶

The Differential Equation¶

Homogenous Poisson Equation¶

Discete Grid¶

Boundary Conditions¶

Numerical Method¶

Matrix form¶

Results¶

Consistency and Convergence¶

Consistency¶

Consitency (Definition)¶

Proof of Consistency¶

Convergence¶

Definition¶

Theorem (DISCRETE MAXIMUM PRINCIPLE).¶

Propositions¶

Definition¶

Lemma¶

Convergence Theorem¶