Supplementary Examples - 3rd Order Taylor Method¶

This notebook illustrates the 3rd order Taylor method using the initial value problem $$ y^{'}=t-y, \ \ (1 \leq t \leq 3) $$ with the initial condition $$y(1)=\frac{2}{e}$$

3rd Order Taylor:¶

The general form of the 3rd order Taylor is: $$ w_{i+1}=w_i+h\left[f(t_i,w_i)+\frac{h}{2}f'(t_i,w_i)+\frac{h^2}{6}f''(t_i,w_i)\right]$$

Read in Libraries¶

import numpy as np
import math 

%matplotlib inline
import matplotlib.pyplot as plt # side-stepping mpl backend
import matplotlib.gridspec as gridspec # subplots
import warnings
import pandas as pd
warnings.filterwarnings("ignore")

Setting up the discrete time axis¶

\[ h=\frac{t_{end}-t_{start}}{N} \]

\[ h=\frac{3-1}{10}=0.2 \]

\[t_i=t_0+ih\]

\[t_i=0+0.2i\]

for $i=0,1,2,...,5.$

N=10
t_end=3.0
t_start=1.0
h=((t_end-t_start)/N)

IC=2/np.exp(1)
t=np.arange(t_start,t_end+h/2,h)
fig = plt.figure(figsize=(10,4))
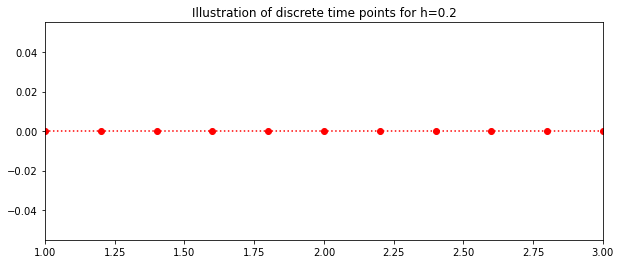
plt.plot(t,0*t,'o:',color='red')
plt.xlim((1,3))
plt.title('Illustration of discrete time points for h=%s'%(h))

Text(0.5, 1.0, 'Illustration of discrete time points for h=0.2')

../_images/203_3rd Order_Taylor_Supplementary_Examples_4_1.png

Specific 3rd Order Taylor¶

To write the specific difference equation for the intial value problem we need derive $f$, $f'$ and $f''$.

\[f(t,y)=t-y\]

def myfun(t,w):
    ftw=t-w
    return ftw

\[f'(t,y)=1-y'=1-t+y\]

def myfund(t,w):
    ftw=1-t+w
    return ftw

\[f''(t,y)=-1+y'=-1+t-y\]

def myfundd(t,w):
    ftw=-1+t-w
    return ftw

Specific Difference equation¶

This gives the difference equation $$ w_{i+1}= w_{i} + h(t_i-w_i+\frac{h}{2}(1-t_i+w_i)+\frac{h^2}{6}(-1+t_i-w_i)) $$

Method¶

Taylor=np.zeros(N+1)
Taylor[0]=IC
y=(2)*np.exp(-t)+t-1
for i in range (0,N):
    Taylor[i+1]=Taylor[i]+h*(myfun(t[i],Taylor[i])+h/2*myfund(t[i],Taylor[i])+h*h/6*myfundd(t[i],Taylor[i]))

Results¶

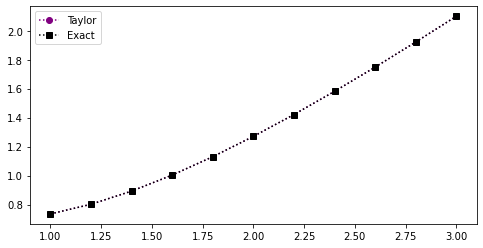
fig = plt.figure(figsize=(8,4))
plt.plot(t,Taylor,'o:',color='purple',label='Taylor')
plt.plot(t,y,'s:',color='black',label='Exact')
plt.legend(loc='best')

<matplotlib.legend.Legend at 0x7fc810583d90>

../_images/203_3rd Order_Taylor_Supplementary_Examples_15_1.png

Table¶

d = {'time t_i': t[0:10],    'Taulor (w_i) ':Taylor[0:10],'Exact (y)':y[0:10],'Exact Error (|y-w|)':np.abs(np.round(y[0:10]-Taylor[0:10],5))}
df = pd.DataFrame(data=d)
df

	time t_i	Taulor (w_i)	Exact (y)	Exact Error (\|y-w\|)
0	1.0	0.735759	0.735759	0.00000
1	1.2	0.802341	0.802388	0.00005
2	1.4	0.893117	0.893194	0.00008
3	1.6	1.003698	1.003793	0.00009
4	1.8	1.130494	1.130598	0.00010
5	2.0	1.270565	1.270671	0.00011
6	2.2	1.421502	1.421606	0.00010
7	2.4	1.581337	1.581436	0.00010
8	2.6	1.748454	1.748547	0.00009
9	2.8	1.921534	1.921620	0.00009

Numerical Analysis