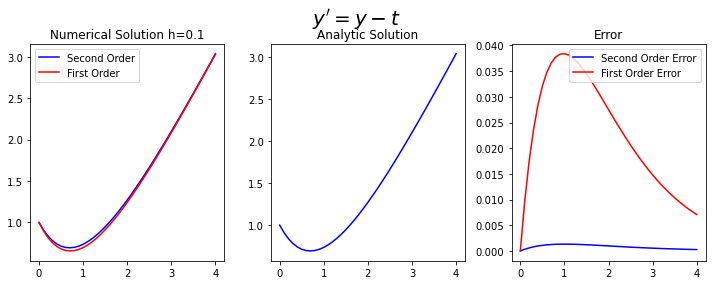
1st vs 2nd order Taylor methods¶
Intial Value Poblem¶
The general form of the population growth differential equation $\( y^{'}=t-y, \ \ (0 \leq t \leq 4) \)\( with the initial condition \)\(x(0)=1\)\( For N=4 with the analytic (exact) solution \)\( y= 2e^{-t}+t+1\)$
Taylor Solution¶
\[ f(t,y)=t-y \]
\[ f'(t,y)=1-y'=1-t+y \]
\[T^1(t_i,w,i)=f(t_i,w_i)=t_i-w_i\]
\[T^2(t_i,w,i)=f(t_i,w_i)+\frac{h}{2}f'(t_i,w_i)=t_i-w_i+\frac{h}{2}(1-t_i+w_i)\]
The first order Taylor difference equation, which is identical to the Euler method, is $\(w_{i+1}=w_i+h(t_i-w_i). \)\( The second order Taylor difference equation is \)\(w_{i+1}=w_i+h(t_i-w_i+\frac{h}{2}(1-t_i+w_i)). \)$
import numpy as np
import math
%matplotlib inline
import matplotlib.pyplot as plt # side-stepping mpl backend
import matplotlib.gridspec as gridspec # subplots
import warnings
warnings.filterwarnings("ignore")
def Second_order_taylor(N,IC):
x_end=4
x_start=0
INTITIAL_CONDITION=IC
h=x_end/(N)
N=N+1;
Numerical_Solution=np.zeros(N)
Numerical_Solution_first=np.zeros(N)
t=np.zeros(N)
Analytic_Solution=np.zeros(N)
Upper_bound=np.zeros(N)
t[0]=x_start
Numerical_Solution[0]=INTITIAL_CONDITION
Numerical_Solution_first[0]=INTITIAL_CONDITION
Analytic_Solution[0]=INTITIAL_CONDITION
for i in range (1,N):
Numerical_Solution_first[i]=Numerical_Solution_first[i-1]+h*(t[i-1]-Numerical_Solution_first[i-1])
Numerical_Solution[i]=Numerical_Solution[i-1]+h*(t[i-1]-Numerical_Solution[i-1]+h/2*(1-t[i-1]+Numerical_Solution[i-1]))
t[i]=t[i-1]+h
Analytic_Solution[i]=2*math.exp(-t[i])+t[i]-1
fig = plt.figure(figsize=(10,4))
# --- left hand plot
ax = fig.add_subplot(1,3,1)
plt.plot(t,Numerical_Solution,color='blue',label='Second Order')
plt.plot(t,Numerical_Solution_first,color='red',label='First Order')
plt.legend(loc='best')
plt.title('Numerical Solution h=%s'%(h))
# --- right hand plot
ax = fig.add_subplot(1,3,2)
plt.plot(t,Analytic_Solution,color='blue')
plt.title('Analytic Solution')
#ax.legend(loc='best')
ax = fig.add_subplot(1,3,3)
plt.plot(t,np.abs(Analytic_Solution-Numerical_Solution),color='blue',label='Second Order Error')
plt.plot(t,np.abs(Analytic_Solution-Numerical_Solution_first),color='red',label='First Order Error')
plt.title('Error')
plt.legend(loc='best')
# --- title, explanatory text and save
# --- title, explanatory text and save
fig.suptitle(r"$y'=y-t$", fontsize=20)
plt.tight_layout()
plt.subplots_adjust(top=0.85)
print(Analytic_Solution)
print(Numerical_Solution)
Second_order_taylor(40,1)
[1. 0.90967484 0.83746151 0.78163644 0.74064009 0.71306132
0.69762327 0.69317061 0.69865793 0.71313932 0.73575888 0.76574217
0.80238842 0.84506359 0.89319393 0.94626032 1.00379304 1.06536705
1.13059778 1.19913724 1.27067057 1.34491286 1.42160632 1.50051769
1.58143591 1.66417 1.74854716 1.83441103 1.92162013 2.01004644
2.09957414 2.1900984 2.28152441 2.37376633 2.46674654 2.56039477
2.65464744 2.74944705 2.84474154 2.94048382 3.03663128]
[1. 0.91 0.83805 0.78243525 0.7416039 0.71415153
0.69880714 0.69442046 0.69995051 0.71445522 0.73708197 0.76705918
0.80368856 0.84633815 0.89443602 0.9474646 1.00495546 1.06648469
1.13166865 1.20016013 1.27164492 1.34583865 1.42248398 1.501348
1.58221994 1.66490904 1.74924269 1.83506463 1.92223349 2.01062131
2.10011228 2.19060162 2.28199446 2.37420499 2.46715552 2.56077574
2.65500205 2.74977685 2.84504805 2.94076849 3.03689548]